Wie du die Streuung deiner Verbrauchswerte kontrollierst.
Die Streuung von Kraftstoffverbrauchswerten kann durch die Berechnung der Standardabweichung und des Vertrauensbereiches der Normalverteilung beurteilt werden.
Wie genau ist der von dir berechnete Durchschnittsverbrauch?
Kannst du diesem Wert vertrauen oder ist er zu ungenau?
Diese Frage stellt sich vor allem dann, wenn du Kraftstoffverbrauchswerte miteinander vergleichen willst, um Schlussfolgerungen aus dem Unterschied zu ziehen.
Ist die Streuung der Werte zu groß, dann kann es zu falschen Schlussfolgerungen führen. Deshalb musst du die Streuung kontrollieren.
In diesem Artikel werde ich erklären, wie du die Standardabweichung berechnen und beurteilen kannst. Du wirst erfahren, warum sie als Maß für die Streuung geeignet ist und wie sie dir bei der Einschätzung eines möglichen Fehlers hilft.
Ich werde auch auf den Vertrauensbereich deiner Stichprobe eingehen. Mit ihm ist es möglich, die Abschätzung eines möglichen Fehlers weiter zu präzisieren.
Um die hier vorgestellten Schritte durchführen zu können, musst du vorher mit der Flottenmonitoring-Methode Kraftstoffverbrauchswerte gesammelt und ausgerechnet und daraus deine Durchschnittsverbrauchswerte berechnet haben.
Wenn du das noch nicht gemacht hast, dann schau gerne nochmal in den entsprechenden Artikeln nach. Die Links bringen dich direkt zu dem jeweiligen Thema.
Am Ende von diesem Artikel kannst du bei mir kostenlos eine Excel-Datei bestellen, mit der du deine eigenen Werte berechnen kannst.
Die Erklärung, warum der Kraftstoff überhaupt streut, findest du im Artikel: »Warum der Kraftstoffverbrauch streut. (einfach erklärt)«.
Aber nun lass uns anfangen.
Warum ist der Durchschnittsverbrauch nicht notwendigerweise genau?
Wir wissen, dass die Streuung von Kraftstoffverbrauchswerten durch eine Normalfunktion abgebildet werden kann. Darum kannst du viele Verbrauchswerte zu einem oder zu wenigen Durchschnittsverbrauchswerten zusammenführen. (Warum das so ist, habe ich im Artikel über die Normalverteilung beschrieben.)
Damit ist es möglich, wenige, repräsentative Kraftstoffverbrauchswerten miteinander zu vergleichen.
Nun hast du leider für die Berechnung der Durchschnittsverbräuche nie alle Werte, die zu deinen Normalfunktionen gehören, zur Verfügung.
Du verfügst immer nur über eine Stichprobe.
Das kann ein Problem mit der Genauigkeit des Mittelwertes der Normalfunktion verursachen. Deshalb müssen wir uns das hier jetzt mal genauer anschauen.
Was ist eine Stichprobe?
Eine Stichprobe ist:
1. Teil einer Gesamtheit, der nach einem bestimmten Auswahlverfahren zustande gekommen ist,
2. Untersuchung, Kontrolle einer Stichprobe, um daraus auf das Ganze zu schließen.
Duden
Die Einzelverbrauchswerte, die du beim Flottenmonitoring sammelst, stellen eine Teilmenge aller möglichen Verbrauchsdaten dar. Deshalb sind sie eine Stichprobe aus der Grundgesamtheit der Verteilungsfunktion.
Und ja, wir wollen aus dieser Stichprobe auf das Ganze schließen!
Um genau zu sein, ist es eine Zufallsstichprobe. Weil das Auswahlverfahren eine zufällige Auswahl ist.
Das ist eine gute Nachricht, denn Zufallsstichproben sind in der Regel weniger von systematischen Fehlern betroffen. Der Zufall mag halt den Zufall.
Was ist der Grund für die Ungenauigkeit des Durchschnittsverbrauches?
In einer Normalverteilung ist zwar die Wahrscheinlichkeit des Auftretens jedes Wertes bestimmt, die Reihenfolge des Auftretens aber nicht.
Aus diesem Grund weiß man nicht, in welcher Reihenfolge der Zufall die Werte in die Stichprobe einspielt.
Meint er es gut mit dir, dann sind die häufigsten Werte der Normalverteilung auch am häufigsten in deiner Stichprobe enthalten.
Die Abweichung zwischen deinem Mittelwert und dem wahren Wert der Normalverteilung ist dann gering und du kannst unbekümmert mit dem Wert arbeiten.
Es kann aber auch sein, dass dir der Zufall zuerst die exotischen Werte auf den Tisch legt.
Dann kann es eine deutliche Abweichung zwischen dem Durchschnittsverbrauch und dem wahren Wert der Normalverteilung geben. Der Wert, den du errechnet hast (Durchschnittsverbrauch), repräsentiert dann nicht die Gesamtheit aller Werte der Grundgesamtheit!
Es gibt keine praktikable Möglichkeit den wahren Wert genau herauszufinden und damit können wir auch nicht sagen, wie groß die Abweichung genau ist.
Weil die Verteilung eine Normalverteilung ist, kannst du abschätzen, wie groß der Bereich um den berechneten Mittelwert ist, in dem sich der wahre Wert mit einer gewissen Wahrscheinlichkeit befindet.
Welche Parameter beeinflussen die Genauigkeit?
Die Streuung der Grundgesamtheit.
Die Größe der Streuung der Grundgesamtheit hat einen Einfluss auf die mögliche Abweichung des Mittelwertes der Stichprobe.
Diese Streuung kommt aus dem Einsatz und hat erstmal nichts mit der Stichprobe zu tun.
Sind die Bedingungen während der Fahrten immer sehr ähnlich, zum Beispiel im Werkverkehr mit viel Autobahn, dann ist die Streuung der Werte klein.
Sind die Bedingungen sehr unterschiedlich, wie zum Beispiel im Einsatz auf einer Baustelle, dann ist die Streuung der Werte groß.
Es ist logisch. Wenn aus dem Einsatz der Fahrzeuge schon eine große Streuung kommt, dann wird natürlich auch die Streuung unserer Stichprobe groß sein.
Normalerweise werden wir uns damit abfinden.
In einigen Fällen kann es aber sinnvoll sein, aus einer Verteilung mehrere zu machen. Also die Einsatzprofile aufzuteilen.
Die Anzahl der Einzelwerte.
Um so mehr Werte du in der Stichprobe hast, um größer ist die Wahrscheinlichkeit, dass die Werte mit einer hohen Auftretenswahrscheinlichkeit auch in der Stichprobe häufig auftreten.
Das ist auch wieder logisch. Der Zufall hält sich an seine eigenen Regeln.
Die Standardabweichung vom Durchschnittsverbrauch – eine Kennzahl für die Streuung.
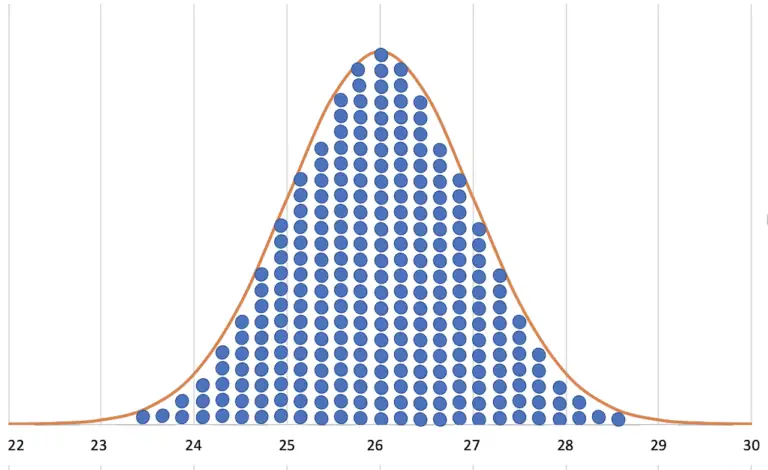
Im Artikel über die Normalverteilung habe ich die Standardabweichung erwähnt. Sie ist ein Maß für die Bauchigkeit der Dichtefunktion.
Hier schauen wir uns nun an, wie man sie berechnet und wie sie uns bei der Beurteilung der Güte des Durchschnittsverbrauches hilft.

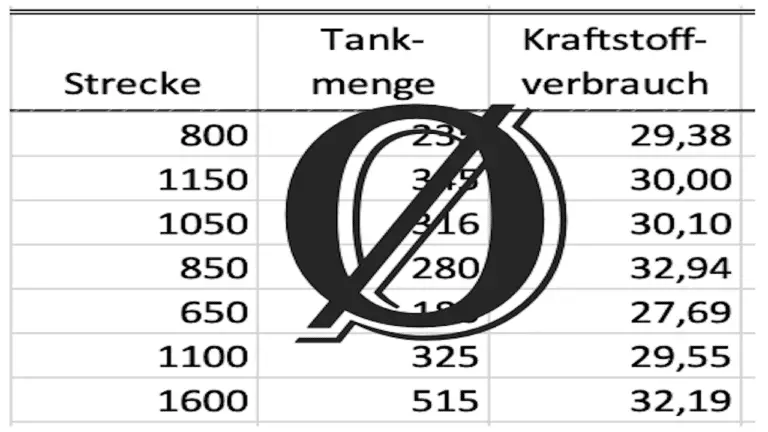
Die Standardabweichung wird berechnet, indem die Differenz zwischen jedem Einzelwert und dem Mittelwert ausgerechnet wird. Diese dann ins Quadrat setzen, aufaddieren, durch die Anzahl der Messwerte minus eins teilen und daraus die Wurzel ziehen.
Berechnung der Streuung
Glücklicherweise gibt es die Standardabweichung direkt als Formel in Microsoft Excel:
=STABW.S()
Im Artikel über die Berechnung des Durchschnittsverbrauches habe ich ein Beispiel gezeigt, in dem ich den Durchschnittsverbrauch aus 5 stark streuenden Einzelwerten berechnet habe. Der Mittelwert war 30,52 l/100 km.
Die dazugehörige Berechnung der Standardabweichung sieht dann so aus:
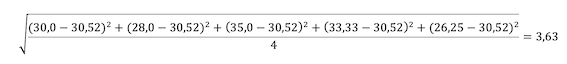
Nun kennst du also den Mittelwert (Durchschnittsverbrauch) und die Standardabweichung. Damit hast du nun zwei Möglichkeiten:
- Du kannst die Dichtefunktionen der Normalverteilung übereinander zeichnen und daraus Schlussfolgerungen über die möglichen Fehler ziehen.
- Du kannst den „Vertrauensbereich“ ausrechnen. Das ist der Bereich um den Mittelwert, indem der wahre Wert mit einer gewissen Wahrscheinlichkeit liegt.
Den zweiten Schritt solltest du machen, wenn du mit dem ersten Schritt zu keinem zuverlässigen Ergebnis kommst.
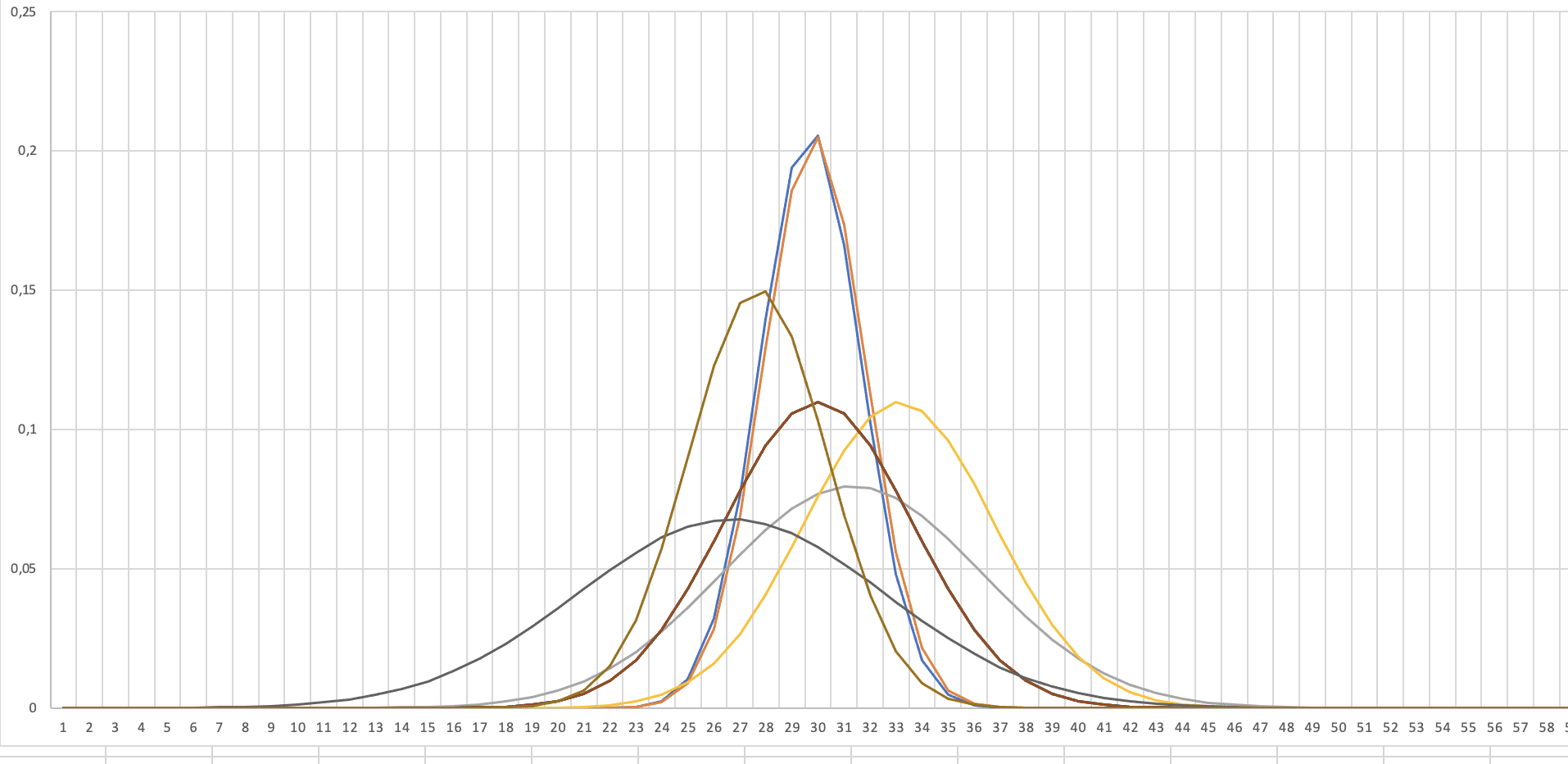
Die Normalverteilungsfunktionen beurteilen.
Wenn du die Dichtefunktionskurven der Gruppen der Kraftstoffverbrauchswerte, die du vergleichen willst, übereinander zeichnest, dann kannst du die Verbrauchstendenz abschätzen.
Schauen wir uns nun mal einige mögliche Konstellationen in Beispielen an.
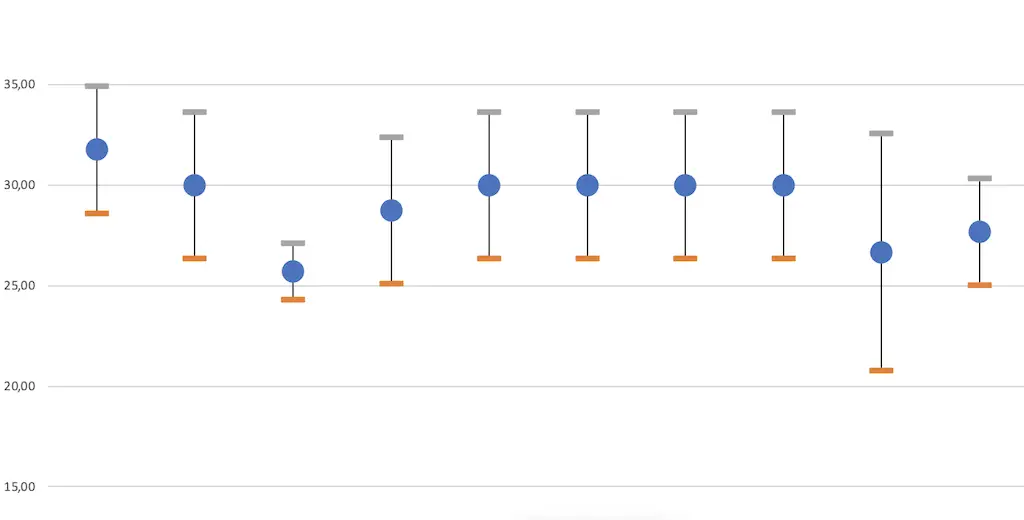
Fall 1: Die Streuung ist gleich groß, die Durchschnittsverbräuche liegen weiter als die Streuung auseinander.
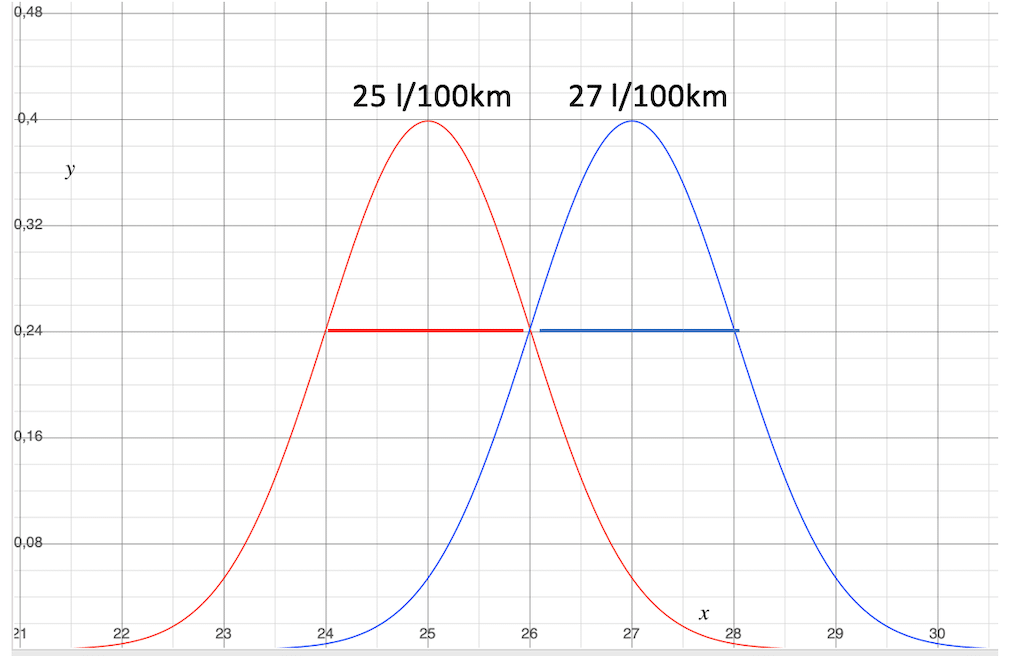
So hätten wir das am liebsten.
Die Standardabweichung der beiden Normalverteilungen ist gleich groß, also ist auch die Streuung der Werte gleich. Das lässt auf vergleichbare Einsatzbedingungen schließen.
Der Unterschied zwischen den Mittelwerten ist gleich groß oder größer als die Streuung der beiden Mittelwerte. Damit kannst du relativ sicher sein, dass der Verbrauch der blauen Gruppen wirklich besser ist, als der Verbrauch der roten Gruppe.
Um das herauszufinden, brauchst du nicht notwendigerweise diese grafische Darstellung. Du siehst das auch, wenn du dir die Zahlenwerte der beiden Verteilungen ansiehst.
Jetzt wo ich dir die Kurven gezeigt haben, kannst du dir sicherlich auch anhand der Zahlenwerte vorstellen, wie das aussieht und musst nicht notwendigerweise die Kurven zeichnen.
Fall 2: Die Streuung ist gleich groß, die Durchschnittsverbräuche liegen innerhalb der Streuung.
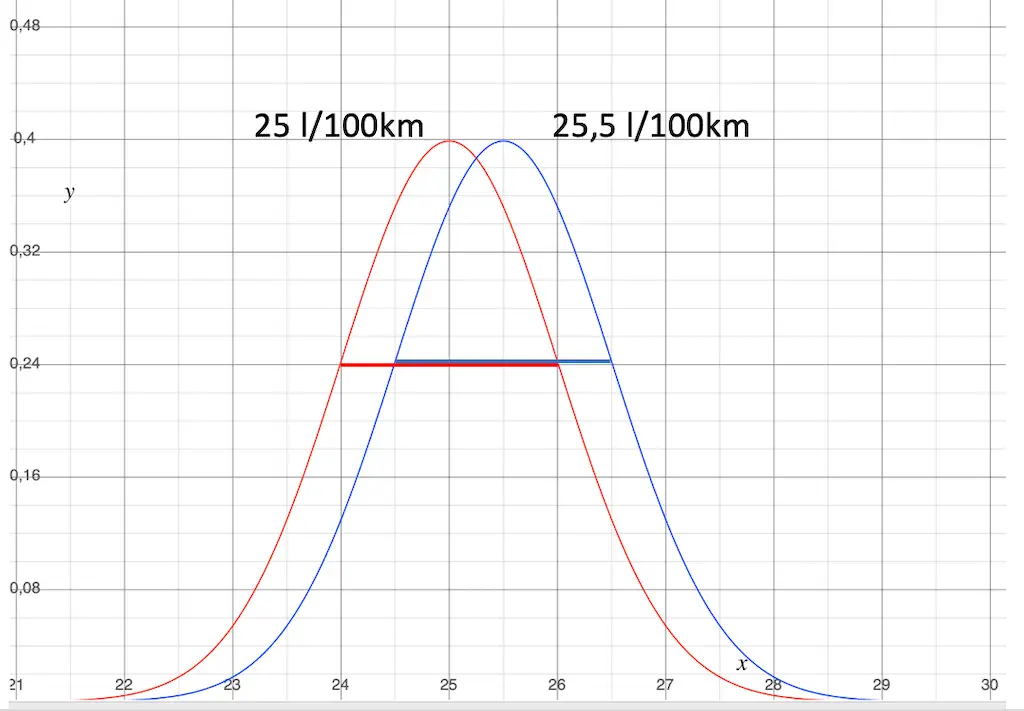
Das sieht nach Bedarf für mehr Analyse aus.
Die Standardabweichung der Normalverteilung ist auch hier gleich groß.
Die Streuung der Werte ist gleich. Die Einsatzbedingungen scheinen kein Problem darzustellen.
Der Unterschied zwischen den Mittelwerten ist hier allerdings mit nur 0,5 l/100 km bedeutend kleiner als die Streuung. Damit kannst du nicht sicher sein, dass der Verbrauch der blauen Gruppen wirklich besser ist, als der Verbrauch der roten Gruppe.
- Wenn der wahre Erwartungswerte der roten Kurven etwas rechts vom roten Mittelwert liegt,
- Wenn dann auch noch der wahre Erwartungswert der blauen Kurve etwas links vom blauen Mittelwert liegt,
- dann wackelt die Schlussfolgerung. Der Verbrauchsunterschied könnte verschwinden oder sich sogar umdrehen.
Bei so einer Situation solltest du mit Schlussfolgerungen vorsichtig sein.
Als Nächstes solltest du den Vertrauensbereich ausrechnen.
Ich erkläre gleich weiter unten, wie das gemacht wird.
Er hilft dir, den Bereich weiter zu präzisieren, in dem der wahre Wert sich befindet. Du kannst dann die Streuung durch den Vertrauensbereich ersetzen.
Wenn auch das nicht zu Klarheit führt, hast du grundsätzlich zwei Möglichkeiten:
Fall 3: Die Streuung ist unterschiedlich groß, die Durchschnittsverbräuche liegen innerhalb der Streuung.
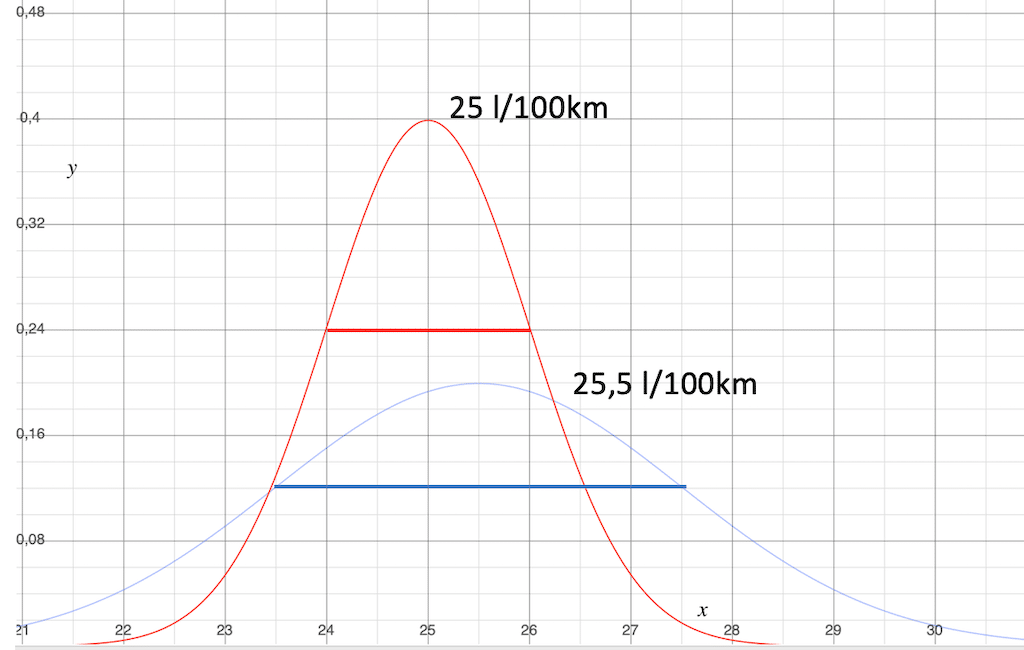
Diese Situation ist sowas wie der statistische SuperGau. Hier müssen wir alle Register ziehen, wenn wir überhaupt eine halbwegs belastbare Aussage herausbekommen wollen.
Die Standardabweichung der Normalverteilung ist deutlich unterschiedlich. Das zwingt uns dazu, die Daten genau zu analysieren.
- Sind die Einsatzbedingungen wirklich so unterschiedlich, dass sich so verschiedene Streuungen einstellen?
- Macht es dann überhaupt Sinn, die Verbrauchswerte miteinander zu vergleichen, wenn der Einsatz so unterschiedlich ist?
- Es können auch Fehler oder systematische Einflussfaktoren dahinter stecken.
Wenn der Einsatz vergleichbar ist und die Streuung trotzdem so unterschiedlich ist, dann stimmt etwas nicht.
Hast du Tankungen vergessen aufzuschreiben? Wirken systematische Einflussfaktoren, die du ausklammern musst, bevor du mit den Daten arbeitest?
In so einem Fall bleibt es dir nicht erspart, tiefer in die Analyse deiner Verbrauchswerte und der Randbedingungen, unter denen sie entstanden sind, abzutauchen.
Findest du bei der Analyse heraus, dass es in den Einsatzfällen Verbrauchswerte gibt, die unter besonderen Umständen entstanden sind, dann sortiere diese Werte aus. Damit kannst du die Streuungen vergleichbarer machen.
Der Unterschied zwischen den Mittelwerten ist mit 0,5 l/100 km auch hier wieder deutlich kleiner als die Streuung.
Damit kannst du nicht sicher sein, dass der Verbrauch der blauen Gruppen wirklich besser ist, als der Verbrauch der roten Gruppe.
Aufgrund der großen Streuung ist die Lage noch unsicherer. Also musst du dich neben den systematischen Faktoren auch noch mit der Statistik befassen.
An dieser Stelle ist auf jeden Fall Vorsicht geboten. Ziehe im Zweifel hier mal lieber keine Schlussfolgerung mit Konsequenzen.
Die Abweichung des Durchschnittswertes vom wahren Wert berechnen.
Bisher haben wir also abgeschätzt, wie sicher der reale Verbrauchsunterschied wahrscheinlich ist.
In der Praxis wird das nach meiner Meinung häufig ausreichen.
Die Mathematiker haben aber noch eine Formel im Programm.
Mit ihr kannst du berechnen, wie groß der Bereich um den Mittelwert ist, in dem sich der wahre Wert mit einer gewissen Wahrscheinlichkeit befindet.
Den Vertrauensbereich der Normalfunktionen berechnen.
Vertrauensbereich um den Durchschnittsverbrauch
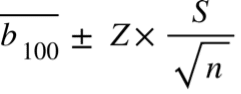

Du nimmst die Standardabweichung deiner Werte und teilst sie durch die Wurzel aus der Anzahl der Werte, aus denen die Stichprobe besteht.
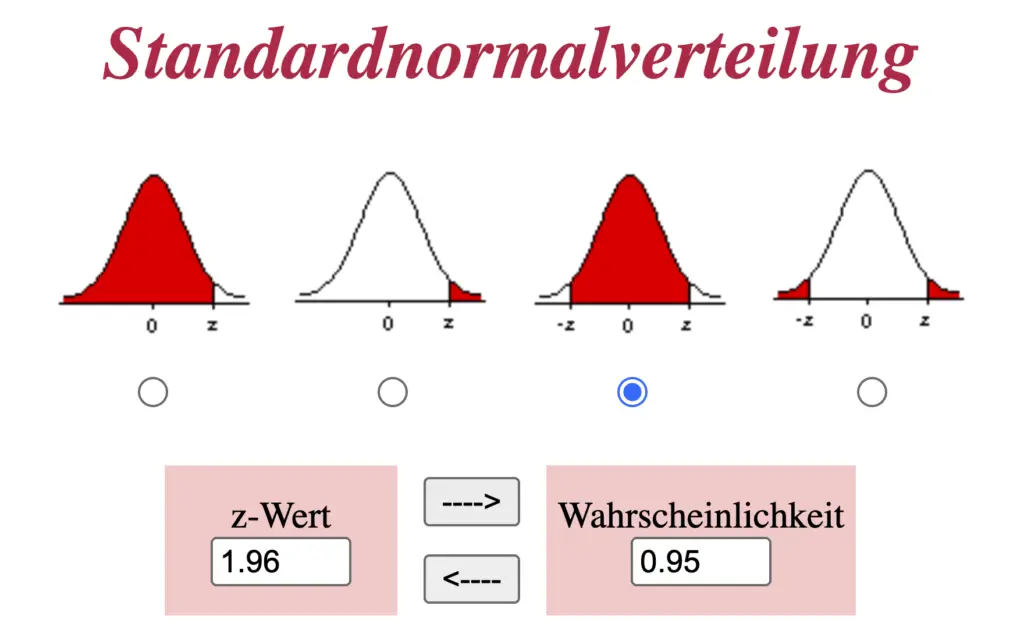
Dann multiplizierst du mit 1,96 und bekommst einen Bereich um den Mittelwert, in dem sich der wahre Wert mit einer Wahrscheinlichkeit von 95 % befindet.
Der Z-Wert für eine Wahrscheinlichkeit von 95 % ist 1,96.
Wenn du den Bereich anderer Wahrscheinlichkeiten berechnen willst, dann kannst du die dazugehörigen Z-Werte auf der Seite der Uni Köln berechnen oder in Tabellen nachschauen.
Auf der Webseite von mathcracker kannst du dein Konfidenzintervall online berechnen.
Hier eine kurze Erklärung der Hintergründe dieser Formel:
Man kann sich vorstellen, dass es unendlich viele Stichproben gibt, die aus ein- und derselben Grundgesamtheit der Verteilung gezogen werden können.
Die Mittelwerte aller dieser Stichproben sind auch wieder normalverteilt.
Das bedeutet, man kann eine Streuung dieser Mittelwerte ausrechnen.
Während die Streuung der Einzelwerte „Standardabweichung“ genannt wird, sagen die Mathematiker zur Streuung der Mittelwerte der Stichproben „Standardfehler“.
Wenn zu diesem Standardfehler noch eine Wahrscheinlichkeit dazugerechnet wird, entsteht daraus die Fehlergrenze und ein Vertrauensbereich.
Der Vertrauensbereich sagt aus, in welchem Bereich um den Mittelwert sich der wahre Erwartungswert mit einer ausgewählten Wahrscheinlichkeit befindet.
Im Artikel zur Berechnung des Durchschnittsverbrauches habe ich als Beispiel den Durchschnittsverbrauch aus 5 stark streuenden Einzelwerten berechnet.
Als Vertrauensbereich mit einer Wahrscheinlichkeit von 95 % errechnet sich hier plus/minus 3,19 l/100 km.
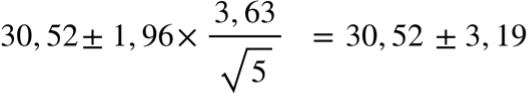
Du siehst, auch bei dieser Betrachtung kommt heraus, dass diese Stichprobe keine Aussagekraft besitzt. Auf der Basis von 5 Werten mit so einer großen Streuung kann man keine Schlussfolgerungen ziehen.
Der wahre Durchschnittsverbrauch wird irgendwo zwischen 27,33 und 33,71 l/100 km liegen und damit eventuell plus/minus 10 % vom Durchschnittsverbrauch entfernt.
Diese Erkenntnis ist auch etwas wert. Ich kann dir sagen, ich kenne Leute, die ziehen Schlussfolgerungen sogar aus einem einzigen Wert und wissen gar nicht, auf was für dünnem Eis sie sich damit bewegen.
Eigentlich darf ich bei weniger als 30 Werten nicht mit dem Z-Wert rechnen.
Ich brauche einen t-Wert, der von der Anzahl der Einzelwerte abhängt. Hier ist eine Tabelle, in der du die t-Werte ablesen kannst.
Zur Auswahl des t-Wertes muss die Anzahl der Werte minus 1 gerechnet werden. In unserem Beispiel gehen ich also in die Zeile mit dem Wert „4“.
Ich will die Wahrscheinlichkeit 95%, also gehe ich in die Spalte „einseitig 0,025, doppelseitig 0,05“ ( 100%- 5% = 95%)
Der t-Wert ist dann 2,776.
Das Vertrauensintervall ist also eigentlich +/- 4,51.
Die Abweichung vom Erwartungswert kann also sogar größer als die Standardabweichung der Einzelwerte sein!
Im Artikel über die Normalverteilung habe ich ein Beispiel von meinem PKW verwendet, bei dem aus 30 Einzelwerten ein Durchschnittsverbrauch von 11,05 l/100 km mit einer Standardabweichung von 1,227 l/100 km herauskam.
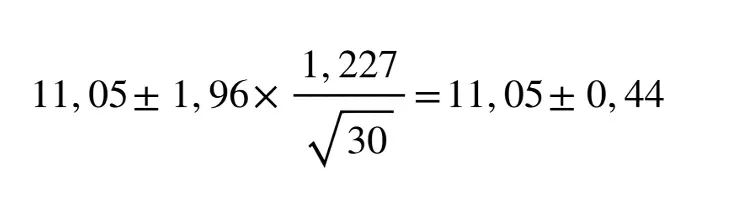
Der wahre Durchschnittsverbrauch liegt hier zwischen 10,61 und 11,49 l/100 km und damit eventuell plus/minus 4 % vom Durchschnittsverbrauch entfernt.
Das ist schon mal wesentlich näher dran. Allerdings wäre auch noch mehr möglich.
Wie kann die Genauigkeit verbessert werden?
Das Wundermittel zur Verbesserung der Genauigkeit ist, mehr Einzelwerte zu beschaffen.
Das ist auch wieder logisch, denn um so mehr Werte die Stichprobe enthält, um so genauer wird sich die richtige Verteilung der Werte einstellen.
Die Werte mit hoher Auftretenswahrscheinlichkeit werden stärker zunehmen, als die Werte mit einer geringen Auftretenswahrscheinlichkeit.
Schauen wir mal, was passiert, wenn wir bei gleicher Streuung mehr Werte hätten.
| Anzahl der Werte (n) | Vertrauensbereich |
| 5 | +/- 3,19 (4,51) |
| 30 | +/- 1.30 |
| 100 | +/- 0,71 |
| 300 | +/- 0,41 |
| 1000 | +/- 0,23 |
Mehr Werte in der Stichprobe verkleinern den Vertrauensbereich.
Das ist gut, denn ein engerer Bereich heißt, dass die Wahrscheinlichkeit steigt, dass der Mittelwert nahe am wahren Durchschnittsverbrauch dran ist.
Ich habe zu Demonstrationszwecken nur die Anzahl der Werte erhöht. Das geht natürlich so nicht. Du musst wirklich mehr Einzelverbrauchswerte einfahren.
Das wird zusätzlich noch die Standardabweichung der Stichprobe verkleinern. Dadurch wird der Vertrauensbereich nochmal enger.
Es ist an der Tabelle schon zu erkennen, dass die Genauigkeit mit steigender Werteanzahl immer weniger zunimmt.
Das ist eine gute Nachricht!
Es bedeutet, dass die unendlich vielen Einzelwerte in der Grundgesamtheit mit einigen hundert Werten in der Stichprobe schon ganz gut erfasst werden können.
Der systematische Fehler darf nicht vergessen werden!
Systematische Fehler können mit dieser Berechnung nicht gefunden werden! Deshalb ist eine weitere inhaltliche Analyse der Messwerte und der Durchführung der Messung notwendig!
Leider bedeutet die Kenntnis vom Vertrauensbereiche des Mittelwertes nicht, dass nicht größere systematische Fehler aufgetreten sein können.
Darum musst du dir die Werte und die Einsatzbedingungen, aus denen die Werte stammen, trotzdem genau anschauen, auch wenn der Vertrauensbereich klein ist.
Einige dieser möglichen Fehler habe ich schon in den Artikeln zur Durchschnittsberechnung und zur Messung von Strecke und Dieselvolumen beschrieben.
Die Spannweite der Daten ist keine aussagefähige Information.
Die Streuung ist nicht mit der Spannweite zu verwechseln, die manchmal landläufig auch als Streuung bezeichnet wird.
Die Spannweite ist der Bereich vom niedrigsten bis zum höchsten Einzelwert. Sie ist einfach auszurechen, sagt aber wenig aus, da schon einzelne „Ausreißer“ den Wert stark beeinflussen.
Das ist mal eine gute Nachricht. Den Wert, der die größte Unsicherheit suggeriert, können wir einfach vernachlässigen.
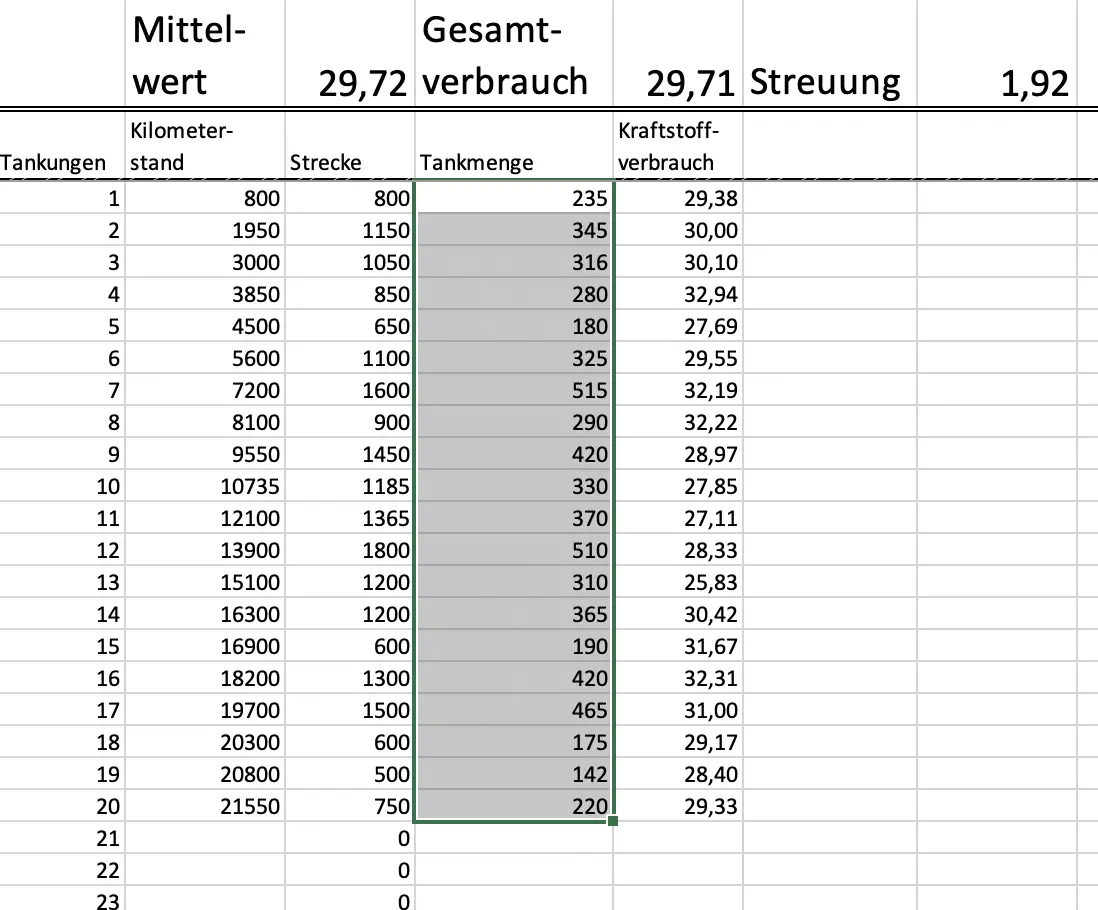
Mein Berechnungstool für dich.
Wenn du mir eine E-Mail schreibst, kannst du von mir ein Excel Datei zum Berechnen und zeichnen der Verteilungen und der Vertrauensbereiche bekommen. Du gibst deine Einzelwerte ein und die Tabelle rechnet Mittelwert, Gesamtverbrauch, Streuung und Vertrauensbereich aus.

Zusammenfassung
Schreibe mir doch bitte im Kommentar, wie dir der Artikel gefallen hat und über welche Themen ich noch schreiben sollte.