Die Normalverteilung – so lässt sich der Zufall berechnen.
Die Streuung von Zufalls-beeinflussten Werten folgt mathematischen Gesetzen, die durch Verteilungsfunktionen beschrieben sind. Die Eigenschaften dieser Funktionen ermöglichen es, die Auftretenswahrscheinlichkeit von Einzelwerten zu berechnen. Von allen Verteilungsfunktionen ist die Normalfunktion vermutlich die wichtigste, weil sie in sehr vielen Anwendungsfällen verwendet werden kann.
Es wäre doch wirklich Klasse, wenn du den Zufall beeinflussen könntest.
Du würdest den Zufall natürlich so einstellen, dass du soviel Geld wie möglich verdienst.
In Bezug auf den Kraftstoffverbrauch würdest du alle zufälligen Verbrauchsfaktoren so einregeln, dass der geringste Kraftstoffverbrauch eintritt.
… geht aber leider nicht!
Du kannst nur die systematischen Verbrauchsfaktoren verändern, auf die zufälligen Faktoren hast du keinen Einfluss. Der Zufall lässt sich von dir nicht hineinreden.
Wusstest du aber schon, dass der Zufall trotzdem festen Gesetzmäßigkeiten folgt?
Auch wenn du keinen Einfluss auf den Zufall hast, kann er trotzdem nicht machen, was er will. Das Universum hat Regeln, an die er sich halten muss und die Naturwissenschaftler haben sie herausgefunden.
Hier in diesem Artikel erkläre ich diese Gesetzmäßigkeit.
Wir werden uns anschauen, was wir über das Auftreten von Zufallsfaktoren herausfinden können.
Mit diesem Wissen kannst du aus deinen vielen unterschiedlichen Kraftstoffverbrauchwerten einen einzigen repräsentativen Wert machen.
Du kannst anhand der Standardabweichung die Streuung deiner Kraftstoffverbrauchswerte bewerten und die Qualität deines Durchschnittsverbrauchswertes beurteilen.
Wie und warum der Kraftstoffverbrauch streut, kannst du im Artikel: »Warum der Kraftstoffverbrauch streut. (einfach erklärt)« nachlesen.
Die Anwendung der Theorie auf den konkreten Anwendungsfall der Kraftstoffverbrauchsermittlung mit der Flottenmonitoring-Methode findest du im Artikel: »Wie du die Streuung von Verbrauchswerten kontrollierst.«
Also dann lass uns gleich anfangen.
Was ist Zufall?
Zufall ist etwas, was man nicht vorausgesehen hat, was nicht beabsichtigt war, was unerwartet geschah.
Quelle: Duden.de
Wenn du die Definition von „Zufall“ googelst, dann wirst du unterschiedliche Definitionen finden und du wirst sehen, dass Zufall in unterschiedlichem Kontext stattfindet.
Nicht nur in Physik und Mathematik, sondern zum Beispiel auch in der Philosophie, in der Psychologie und sogar in der Rechtswissenschaft.
Mir gefällt die Definition aus dem Duden am besten. Sie erklärt die Herkunft des Wortes „Zufall“:
„zufallen, mittelhochdeutsch zuoval = das, was jemandem zufällt, zuteilwird, zustößt.“
(Quelle: Duden.de)
Zufällig bedeutet also, dass es sich unserer Kontrolle entzieht.
Im physikalisch-technischen Kontext ist ein Ereignis zufällig, wenn ein System so komplex oder unerforscht ist, dass wir es nicht verstehen und darum keine Möglichkeit haben, Einfluss zu nehmen oder sein Verhalten vorherzusagen.
Was ist eine Verteilung?
Die Verteilung einer zufälligen Größe zeigt die Häufigkeit des Auftretens der einzelnen Werte einer Messreihe oder eines Datensatzes.
Ich habe dir zur Veranschaulichung ein Diagramm mitgebracht, in dem ich die Verteilung der Kraftstoffverbrauchswerte meines Autos dargestellt habe. (Ja, ich muss gestehen, es war nicht gerade ein kleines Auto.)
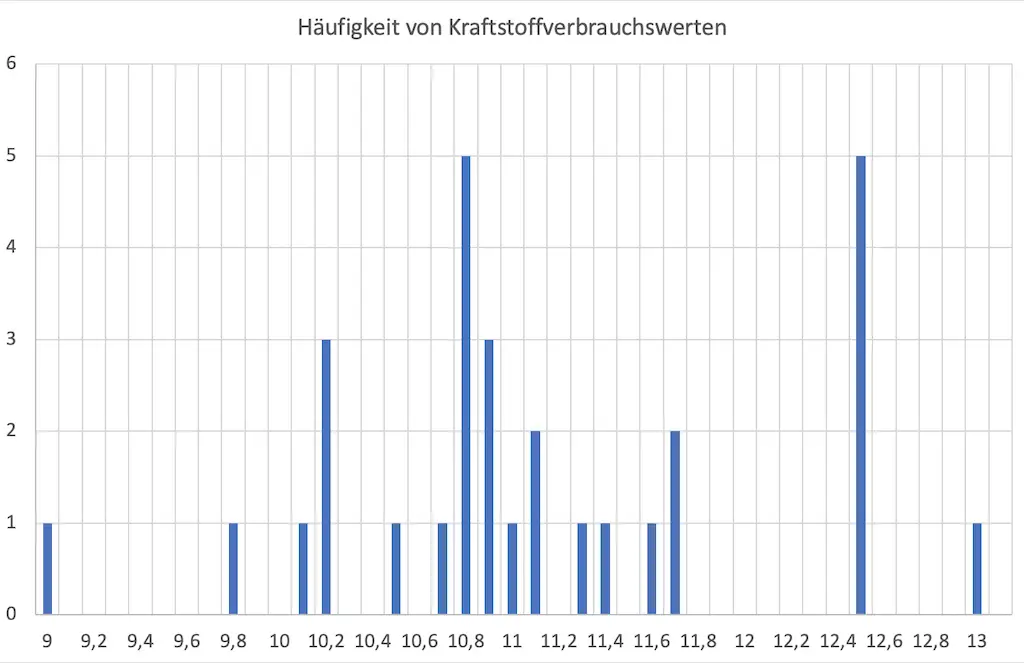
Auf der horizontalen Achse sind die Kraftstoffverbrauchswerte zu finden und auf der vertikalen Achse die Häufigkeit des Auftretens.
Du siehst, dass in meiner Messreihe einige Verbrauchswerte gar nicht aufgetreten sind. 10,8 und 12,5 l/100 km sind jeweils 5-mal gemessen worden und stellen damit die häufigsten Werte dar.
Außer der Erkenntnis, dass Verbrauchswerte zwischen 9 und 13 Liter pro 100 km berechnet wurden, macht uns diese Darstellung aber nicht viel schlauer.
Das liegt daran, dass ich nur 30 Messwerte ermittelt habe.
Hätte ich unendlich viele Messungen, dann würden wir in dieser Darstellung eine mathematische Funktion erkennen können.
Das ist ein typisches Problem. Wir müssen einen anderen Weg finden, wie wir unsere konkrete Funktion herausfinden.
Eine Verteilungsfunktion verrät uns die Auftretenswahrscheinlichkeiten.
Verteilungsfunktionen beschreiben die mathematischen Gesetzmäßigkeiten, nach denen die Häufigkeit von zufälligen Werte auftritt.
Die Auftretenswahrscheinlichkeit von Zufallsgrößen kann mathematisch durch Verteilungsfunktionen beschrieben werden.
Das ist nützlich für uns. Wenn wir wissen, nach welcher Verteilungsfunktion sich eine Zufallsgröße verteilt, dann können wir auch bei einer begrenzten Anzahl von Messwerten die Wahrscheinlichkeit des Auftretens von einzelnen Werten herausfinden.
Die wichtigsten Verteilungsfunktionen kannst du dir auf der Seite von Novustat anschauen: Die 5 wichtigsten Typen der Wahrscheinlichkeitsverteilung – mit Beispielen aus der Praxis
Wenn du dir die Funktionen da anschaust, dann wirst du erkennen, dass die Art der Verteilung der Werte in den verschiedenen Fällen sehr unterschiedlich ist.
Dummerweise gilt fürs Lottospielen die Gleichverteilung. Bei dieser Verteilungsfunktion ist die Wahrscheinlichkeit des Auftretens für alle Werte gleich groß. Also leider werden wir durch die Kenntnis dieser Verteilungsfunktion nicht zum Lottomillionär.
Bei der Normalverteilung ist das anders, da gibt es Werte, die viel häufiger als andere Werte auftreten. Und glücklicherweise gilt für den Kraftstoffverbrauch die Normalverteilung.
Was ist eine Normalverteilung?
Die Normalverteilung ist eine Verteilungsfunktion, die häufig dann auftritt, wenn viele zufällig streuende Einflussfaktoren auf einen Sachverhalt einwirken. Dabei spielt die Art der Verteilung der einzelnen Faktoren keine Rolle.
Quelle: Uni UlM
Den mathematischen Beweis für diese Definition kannst du dir unter dem Link zur Quelle ansehen. Die Mathematiker führen diesen Beweis mithilfe des Grenzwertsatzes. Du kannst es aber auch einfach nur glauben, denn für einen Nichtmathematiker ist das schon sehr anspruchsvoller Stoff.
Weil es sehr häufig solche Sachverhalte mit sehr vielen zufälligen Einflussfaktoren gibt, ist die Normalverteilung sehr oft anwendbar. Hier mal eine paar Beispiel für normalverteilte Sachverhalte:
Auch beim Kraftstoffverbrauch wirken sehr viele zufällige Einflussfaktoren auf den Verbrauchswert ein.
Wir können annehmen, dass die Verteilung von Kraftstoffverbrauchswerten einer Normalverteilung folgt.
Das ist deshalb super, weil die Normalverteilung Eigenschaften hat, die uns sehr helfen werden.
Wer hat die Normalverteilung herausgefunden?
Der deutsche Mathematiker Carl Friedrich Gauß aus Göttingen hat die Normalverteilung und ihre charakteristischen Kenngrößen erforscht.

Seine Entdeckung war bahnbrechend für die Mathematik und hilft uns noch heute bei der Beantwortung von sehr, sehr vielen praktisch relevanten Fragestellungen.
Da sie so häufig zutrifft, hat diese Verteilung den Namen „Normalverteilung“ bekommen. (So nach dem Motto: Normalerweise kannste diese Funktion nehmen.)
Der Verdienst von Gauß ist so groß, dass man die Normalverteilung nach ihm „Gaußverteilung“ nennt.
Die Bedeutung seiner Leistung wurde dadurch gewürdigt, dass Gauß und seine „Glockenkurve“ auf dem alten deutschen 10 Mark Schein abgebildet waren. Der 10 Mark Schein ist Vergangenheit, die Bedeutung der Leistung von Gauß ist geblieben.
Wie sieht die Normalverteilung aus?
Die Normalverteilung kann durch zwei mathematische Funktionen und deren Funktionskurven beschrieben werden:
Die Verteilungsfunktion
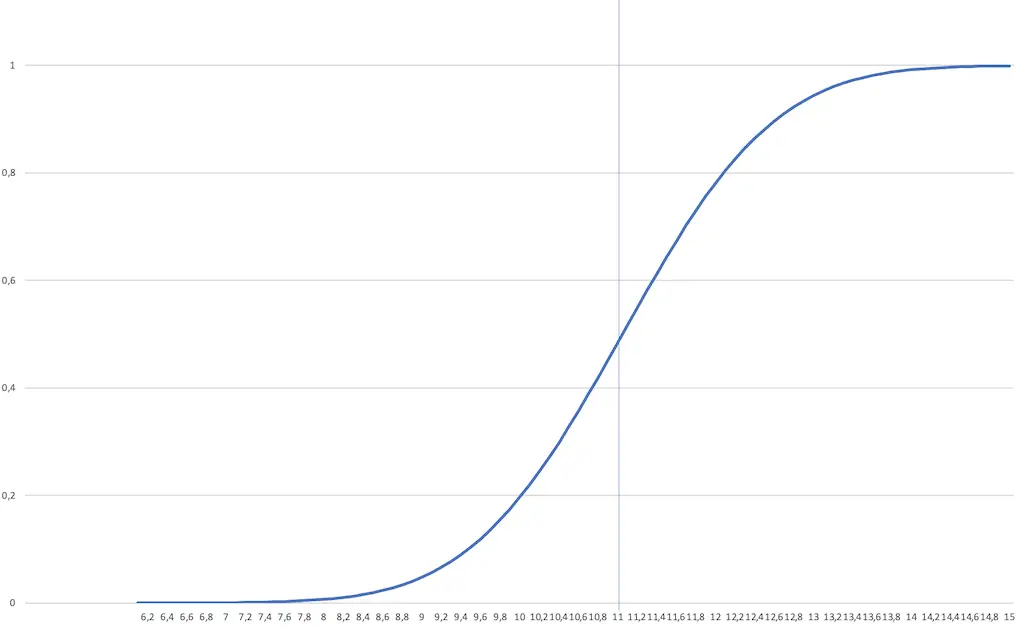
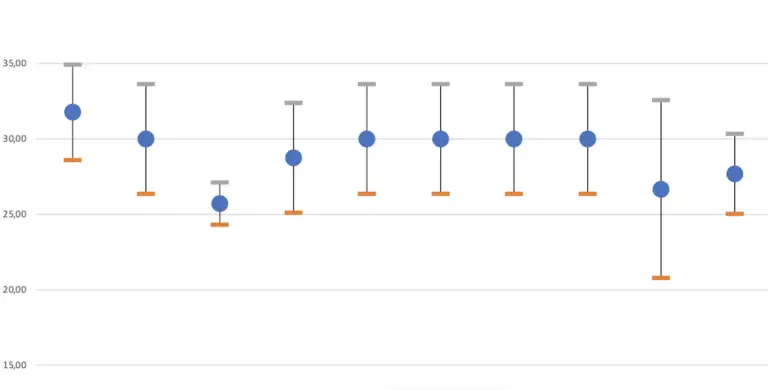
Im Bild der Verteilungsfunktion siehst du die Funktionskurve, die sich ergibt, wenn ich die, zu meinen Messwerten passende, Normalverteilung ausrechne.
Schauen wir uns mal an, was wir hier erkennen können.
Du siehst, dass wir zusätzliche Informationen aus der Verteilungsfunktion ableiten können. So richtig praxisrelevant sind diese Information allerdings immer noch nicht. Deshalb schaut man auch selten auf die Verteilungsfunktion, sondern auf die Dichtefunktion.
Du fragst dich vielleicht, wie ich das so genau ablesen kann. Nun, ich kann das aus der Tabelle ablesen, die ich zum Zeichnen der Funktionskurve verwendet habe.
Die Dichtefunktion
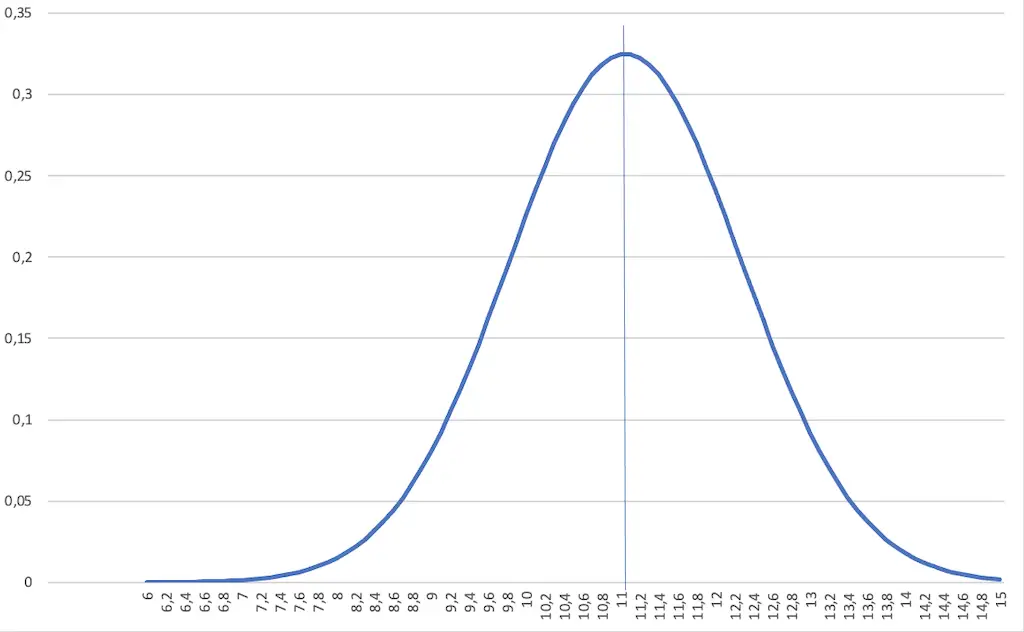
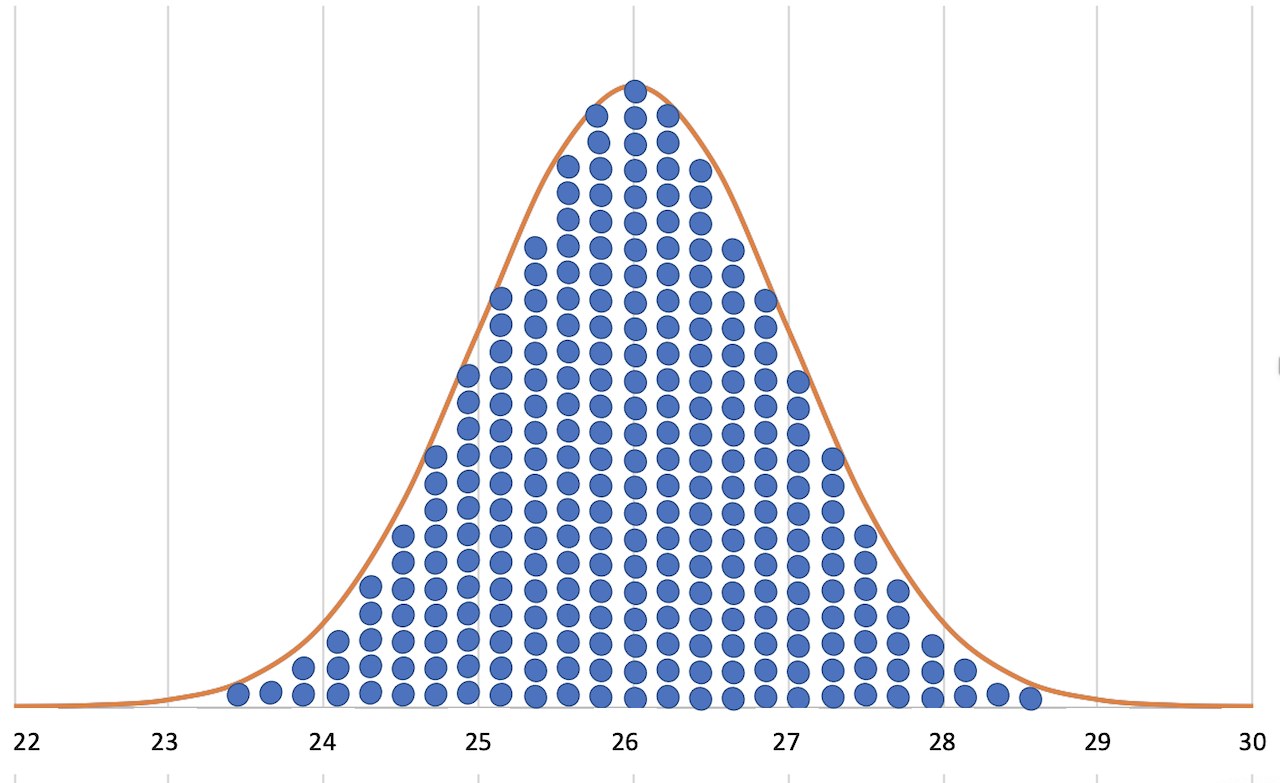
Die Funktionskurve der Dichtefunktion ist die berühmte „Glockenkurve“.
Aufgrund ihrer charakteristischen Eigenschaften sieht die Dichtefunktion der Gaußverteilung wie eine Glocke aus. Sie wird deshalb „Glockenkurve“ genannt.
Wie der Name sagt, zeigt die Dichtefunktion, wie dicht die einzelnen Werte beieinander liegen.
Hat die Kurve eine schmale, schlanke Form, dann liegen die einzelnen Werte dicht beieinander. Das bedeutet, die Streuung ist klein und damit haben die Werte in der Mitte eine hohe Auftretenswahrscheinlichkeit.
Hat die Kurve dagegen eine breite, bauchige Form, dann ist die Streuung groß. Die Auftretenswahrscheinlichkeit von weiter auseinanderliegenden Werte ist relativ hoch.
Die Dichtefunktion der Normalverteilung hat charakteristische Merkmale, die wir nutzen werden.
Was verraten uns die Parameter der Normalverteilung?
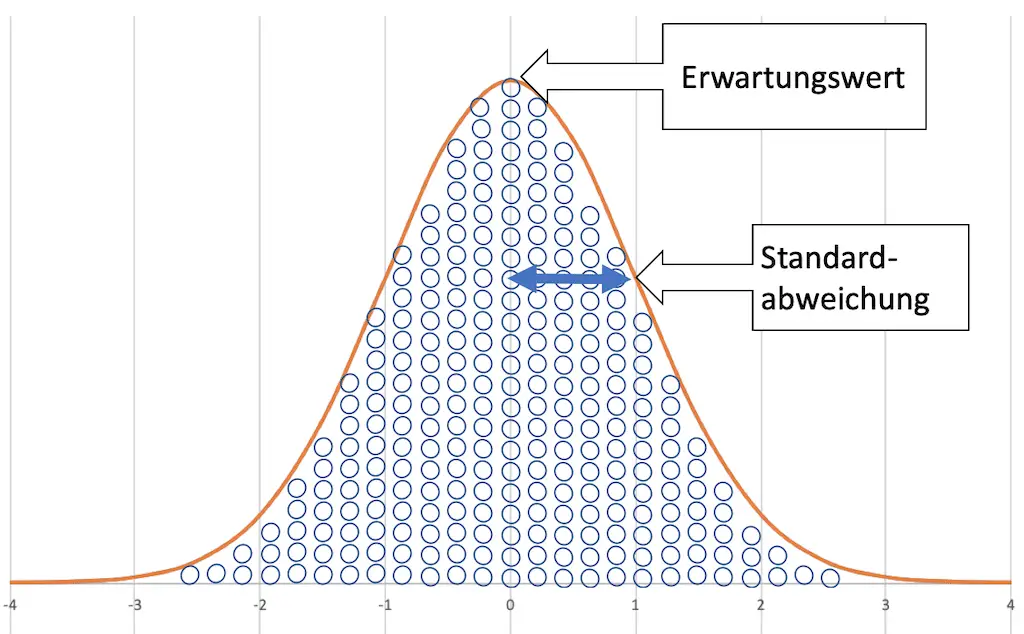
Der Erwartungswert
Er ist sowohl der arithmetische Mittelwert, als auch der Median der Grundgesamtheit aller Werte einer Normalverteilung.
Der Erwartungswert ist der Wert, der mit der größten Häufigkeit auftritt. Er repräsentiert den Durchschnitt aller Werte.
Weil die Kurve symmetrisch zum Erwartungswert ist, treten genauso viele kleinere Werte, wie größere Wert auf. Darum mitteln sich die Werte aus und was übrig bleibt ist der Erwartungswert selber.
Das ist ein riesiger Vorteil! Dadurch können wir alle Werte zu einem einzigen Wert zusammenführen!
Dieser Wert ist das, was du suchst, wenn du deinen Kraftstoffverbrauch wissen willst.
Die vielen Abweichungen, die Streuung verursachen, gleichen sich aus und es bleibt ein einziger Wert übrig, mit dem du arbeiten kannst.
Wir können den Erwartungswert verwenden, denn er steht für den puren, nicht streuenden Verbrauch.
Der repräsentative Kraftstoffverbrauchswert, den wir uns die ganze Zeit wünschen, ist der Erwartungswert der Dichtefunktion der Kraftstoffverbrauchswerte.
Der wahre Wert
Leider hat auch diese Sache einen kleinen, aber bedeutsamen Haken.
Der wahre Mittelwert wird uns immer unbekannt bleiben.
Wenn wir die Dichtefunktion unserer Normalverteilung ausrechnen, dann haben wir nie alle Einzelwerte, die zu unserer Funktion gehören.
Wir haben immer nur einen zufälligen Ausgriff an Werten. Diesen Ausgriff nennt man „Stichprobe“.
Wir können also nicht ganz sicher sein, ob der Mittelwert, den wir ausrechnen, wirklich der absolut korrekte Mittelwert der Normalverteilung ist.
Deshalb wird dieser Wert auch Erwartungswert genannt. Wir erwarten, dass dieser Werte der wahre Mittelwert ist, ganz sicher können wir aber nicht sein.
Also müssen wir überprüfen, wie groß die mögliche Abweichung zwischen unserem Erwartungswert und dem wahren Mittelwert sein kann.
Es gibt Formeln, mit denen du ausrechnen kannst, wie groß der Bereich um den Erwartungswert ist, in dem sich der wahre Wert mit einer gewissen Wahrscheinlichkeit befindet.
Ich halte das aber für wenig hilfreich.
Ein guter Indikator ist die Standardabweichung, denn sie gibt dir eine Information über die Streuung der ganzen Verteilung und damit auch über die Unsicherheit deines Erwartungswertes.
Die Standardabweichung
Die Standardabweichung kennzeichnet die Bauchigkeit der Kurve. Sie stellt die Wendepunkte der Kurve dar. Innerhalb von einer Standardabweichung (nach oben und nach unten) liegen 68 % der Werte.
Die Standardabweichung gibt uns ein Gefühl, wie die Einzelwerte streuen. Damit können wir abschätzen, wie häufig Werte im Bereich des Erwartungswertes auftreten.
Aus diesem Grund können wir die Standardabweichung als Kenngröße verwenden, die uns die Streuung verdeutlicht.
Das Formelzeichen der Standardabweichung ist Sigma. Du hast vielleicht schon mal von „Six Sigma“ gehört.
Im Bereich von 6-mal der Standardabweichung befinden sich 99,99966 % der Werte der Normalverteilung. Es gibt also praktisch keine Werte außerhalb dieses Bereiches.
Man versucht in der Qualitätssicherung den Bereich der Abweichungen von der Norm so gering wie möglich zu haben. Deshalb gibt man sich einen Zielbereich für 6 Standardabweichungen der Normalverteilung des betreffenden Wertes vor. Hat man das erreicht, dann gibt es praktisch keinen Ausschuss mehr.
Für unsere Zwecke reicht einmal Sigma aus. Wir wollen es ja nicht übertreiben.
Normalfunktion zeichnen
Um die Dichtefunktion der konkreten Normalverteilung deiner Kraftstoffverbrauchswerte zu erhalten, musst du die beiden Parameter der Normalverteilung ausrechnen.
Da wir ja die echten Parameter unserer Funktion nicht kennen und wahrscheinlich auch nie herausbekommen werden, wenden wir einen einfachen Trick an.
Wir nehmen einfach die Werte der Stichprobe, die wir haben. Damit berechnen wir den Mittelwert und verwenden ihn als Erwartungswert. Mit der Formel für die Streuung berechnen wir die Standardabweichung unserer Stichprobe.
Die benötigten Formeln findest du im Artikel über die Berechnung des Durchschnittsverbrauches.
Hast du nun diese beiden Werte, dann kannst du dir zum Beispiel auf der Seite von: Wolfram/Alpha Widgets die Kurve zeichnen lassen.
Es gibt in Microsoft Excel eine Formel, die mir die Werte der Normalfunktion berechnet. Das könnte dann so aussehen:
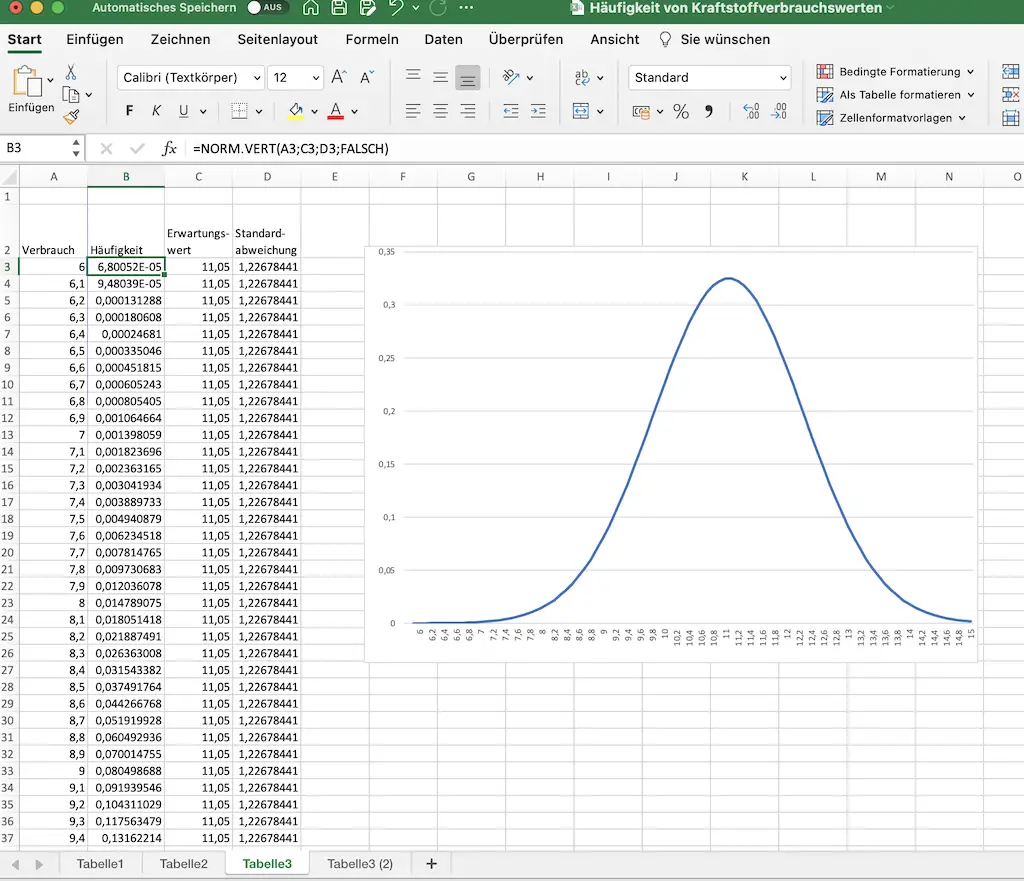
Die Formel heißt NORM.VERT(Wert, Erwartungswert, Standardabweichung. Falsch). Bei Falsch bekommst du die Dichtefunktion, bei wahr bekommst du die Verteilungsfunktion.
Wenn du die abgebildete Datei von mir bekommen möchtest, dann schreibe mir ein E-Mail und ich schicke sie dir kostenlos zu. Als Dank hätte ich gern deine Einwilligung, deine E-Mail-Adresse abspeichern zu dürfen, um dich über neue Artikel zu informieren.