Wie du den Durchschnittsverbrauch richtig ausrechnest.
Es gibt 3 Möglichkeiten, den Durchschnittsverbrauch aus Gruppen von Einzelverbrauchen zu berechnen. Die Berechnung des Mittelwertes, des Gesamtverbrauches und des gewichteten Mittelwertes.
Du sollst immer den Durchschnittsverbrauch aus vielen Einzelwerten berechnen, bevor du ein Urteil fällst.
In meinen Artikeln über das Flottenmanagement habe ich immer wieder darauf hingewiesen, dass du aus einem Einzelverbrauchswert vom normalen Fahrbetrieb keine Schlussfolgerungen ziehen sollst. Er ist viel zu volatil.
In diesem Artikel werde ich dir nun zeigen, wie du den Durchschnittsverbrauch richtig ausrechnest.
Du wirst drei Möglichkeiten der Berechnung finden und die Vor- und Nachteile jeder Variante kennenlernen.
Der Artikel wird dir helfen, die Sinnvollste der drei Möglichkeit für dich auszuwählen.
Damit bist du dann gerüstet in die Verbesserung des Kraftstoffverbrauches einzusteigen und diesen gezielt und systematisch zu verringern.
Lass dich nicht von den Formeln abschrecken, es ist einfach zu rechnen. Ich werde es im Text ganz ausführlich erklären. Solche Formel sehen halt wissenschaftlich aus.
Was ist der Durchschnittsverbrauch?
Auf einigen anderen Webseiten findest du unter dem Begriff „Durchschnittsverbrauch“ den Wert, den ich als den Einzelverbrauchswert bezeichne.
Das ist keine falsche Aussage.
Der Verbrauch auf der Strecke von einem Tankstopp zum nächsten, setzt sich aus mehreren, gemittelten, unbekannten 100-Kilometer-Werten zusammen. Deshalb ist er schon ein Mittelwert aller dieser unbekannten Einzelwerte.
Aber wenn ich für diese Zahl den Namen „Durchschnittsverbrauch“ verwende, wie nenne ich dann den Durchschnitt der Durchschnitte, den wir für die Flottenüberwachung benötigen?
Lass uns der Einfachheit halber folgendes vereinbaren:
Damit können wir die zwei unterschiedlichen Werte mit ihren Stärken und Schwächen auseinander halten.
Der Durchschnittsverbrauch ist der Wert, der beim Flottenmonitoren die zufälligen Kraftstoffverbrauchsfaktoren ausmittelt, weil er nicht nur mehrere hundert, sondern viele tausend Kilometer Fahrstrecke beinhaltet.
Wie Flottenmonitoring zur Kraftstoffverbrauchsermittlung richtig gemacht wird, kannst du im Artikel: Wie du den Kraftstoffverbrauch mit Flottenmonitoring herausfindest nachlesen.
Der durchschnittliche Verbrauch ist die Zahl, die du zum Vergleichen und Verbessern benutzt.
Er kann für einzelne Fahrzeuge, für eine gesamte Fahrzeugflotte oder für eine ausgewählte Gruppe von Fahrzeugen mit gemeinsamen Merkmalen berechnet werden. Es kommt darauf an, was du dir anschauen möchtest:
Als Merkmale dienen systematischen Einflussfaktoren. Ich werde in einem eigenen Artikel noch genauer darauf eingehen, wie das gemacht wird.
Schauen wir uns also nun an, welche Möglichkeiten der Durchschnittswertberechnung es gibt.
Alternative 1 – Der Durchschnittsverbrauch als Mittelwert aus den Einzelverbräuchen
Die naheliegendste und damit wahrscheinlich am häufigsten benutzte Formel ist der Mittelwert.

Beim Mittelwert werden alle Einzelverbrauchswerte aufsummiert und durch die Anzahl der Werte geteilt.
Berechnung des Mittelwertes
In Microsoft Excel gibt es eine eigene Formel für den Mittelwert, die du benutzen kannst.
=MITTELWERT(A1:A10)
In der Spalte A stehen dann jeweils die Einzelverbrauchswerte.
Bei der Mittelwertberechnung geht der Bezug zur Strecke verloren!
Diese Berechnung beinhaltet allerdings ein nicht unerhebliches Fehlerpotential. Deshalb empfehle ich diese Vorgehensweise nur dann anzuwenden, wenn du den Fehler genau kontrollierst!
Wenn du den Durchschnittsverbrauch als Mittelwert aus den Einzelverbräuchen berechnest, geht die Relation des Kraftstoffverbrauches zur gefahrenen Strecke verloren.
Jeder Einzelverbrauchswert wird gleich wichtig genommen.
Das ist schlecht, denn das führt dazu, dass die Häufigkeit des Tankens einen Einfluss auf das Ergebnis der Durchschnittsverbrauchsberechnung bekommt und das ist nicht korrekt.
Es passiert folgendes:
Dieser Fehler tritt immer dann zu Tage, wenn die Einsatzschwere bzw. die Ausladung sehr unterschiedlich ist.
Ich will das an einem Beispiel zeigen.
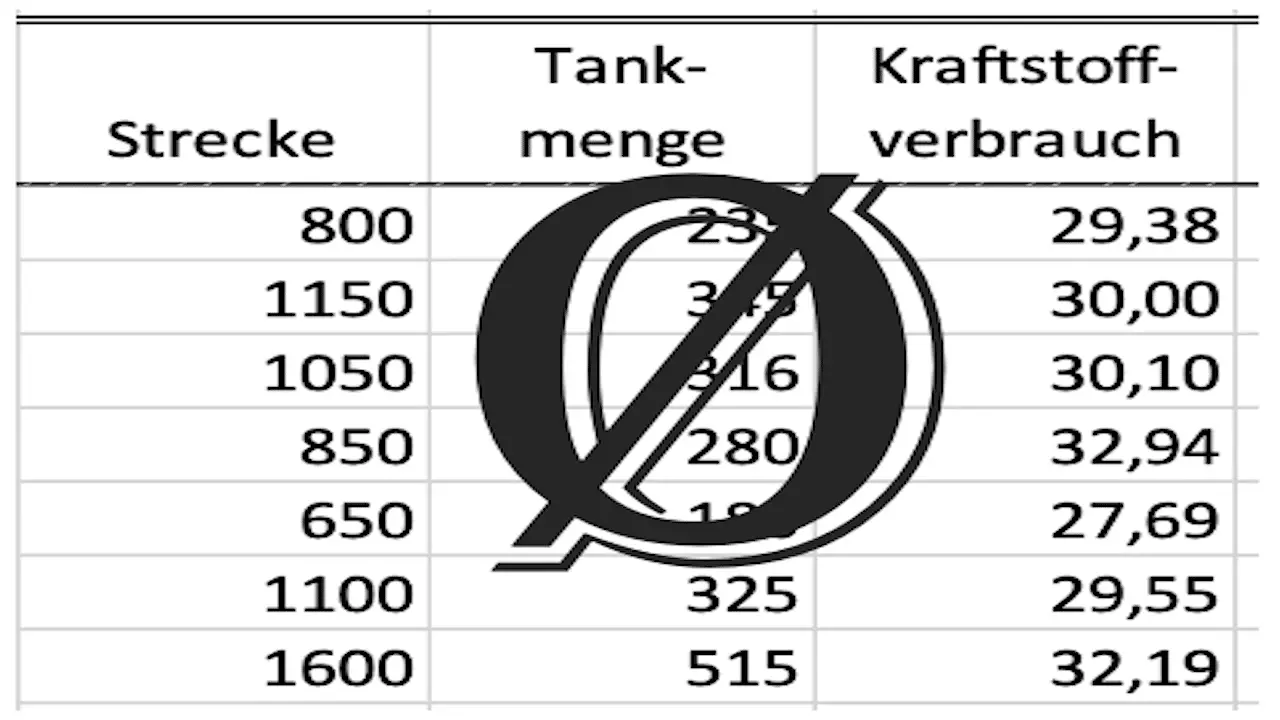
Die Werte in der Tabelle habe ich absichtlich so gewählt, dass dieser Effekt deutlich wird. Ich werde bei allen Beispielrechnungen die gleichen Werte verwenden. Dann können wir am Ende die Ergebnisse vergleichen.
| Tankung | Kilometerstand (km) | Strecke (km) | Dieselmenge (l) | Verbrauch (l/100km) |
| 1 | 300 | 300 | 90 | 30,0 |
| 2 | 800 | 500 | 140 | 28,0 |
| 3 | 1400 | 600 | 210 | 35,0 |
| 4 | 1700 | 300 | 100 | 33,33 |
| 5 | 2500 | 800 | 219 | 26,25 |
Der Mittelwert ist hier:
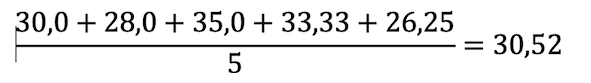
Merk dir diesen Wert, wir werden ihn gleich unten mit den Ergebnissen der anderen Berechnungen vergleichen.
Ist diese Ungenauigkeit akzeptabel?
Da diese Berechnungsmethode wirklich sehr einfach ist, wirst du dir sicherlich überlegen, ob es nicht einen Weg gibt, mit diesem Fehler leben zu können.
Nun, als erstes solltest du beurteilen, wie groß der Fehler in deinem konkreten Fall wirklich ist.
Dazu eignen sich die anderen Berechnungsmethoden als Vergleich.
Ist die Abweichung in deinen typischen Einsatzfällen gering, dann kannst du es vielleicht riskieren.
Einen weiteren Hinweis gibt dir die Streuung, die wir später noch ausrechnen werden. Ist die Streuung der Einzelwerte gering, dann ist auch dieser Fehler klein.
Alternativ kannst du die Tankungen statt an der Strecke, an der Zeit ausrichten.
Wenn du, unabhängig vom Füllstand im Tank, immer zur gleichen Zeit tankst, dann reduziert sich dieser Fehler. Das könnte am Anfang oder Ende jeden Tages oder jeder Schicht sein.
Dafür bekommst du dann eventuell einen Fehler durch die Mischtemperatur. Das sollte aber die bessere Alternative sein, weil sich die Fehlmengen, die dadurch entstehen, ja über die Tankungen ausmitteln. Du darfst natürlich keine Tankung auslassen.
Alternative 2 – Der Durchschnittsverbrauch als Gesamtverbrauch
Eine einfache Alternative, die den Fehler des Mittelwertes umgeht, ist die Berechnung des Durchschnittsverbrauches als Gesamtverbrauch aus der Summe der Strecken und der Summe der Tankmengen.

Beim Gesamtverbrauch werden die Tankmengen und die Fahrstrecken einzeln aufsummiert. Danach wird die Summe der Dieselvolumen durch die Summe der Fahrstrecken geteilt und mit 100 multipliziert.
Berechnung des Gesamtverbrauches
Für diese Berechnung gibt es zwar in Excel keine vordefinierte Formel, sie ist aber ganz einfach zu schreiben:
=100*SUMME(A1:A10)/SUMME(B1:B10)
In der Spalte A stehen die Tankvolumen und in Spalte B die Fahrtstrecken.
Hier das Beispiel für die Gesamtverbrauchsberechnung:
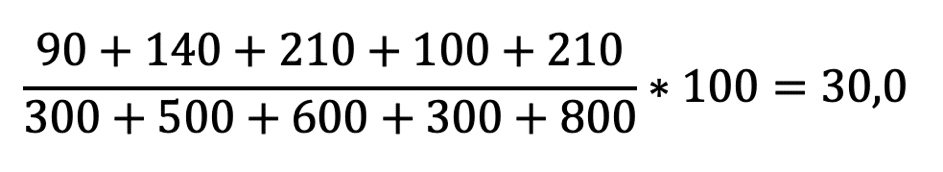
In meinem Beispiel ergibt das den korrekten Durchschnittsverbrauch von 30,0 l/100km.
Der Fehler der Mittelwertberechnung ist also 1,7%, da sind ja 30,52 l/100 km rausgekommen.
Ein drastischer Fehler! Und das, obwohl die einzelnen Verbrauchswerte gar nicht sooooo weit auseinander liegen.
Du siehst also, dass es wichtig ist, sich das genau anzusehen.
Ich empfehle die Berechnung des Gesamtverbrauches zu nutzen, da in der Regel alle Daten verfügbar sind und damit die aufwendige Gewichtung der Mittelwerte vermieden werden kann.
Alternative 3 – Der Durchschnittsverbrauch als gewichteter Mittelwert
Die Berechnung des korrekten, gewichteten Mittelwertes schauen wir uns jetzt an.
Diese Formel gibt jedem Einzelwert seinen korrekten Anteil am Gesamtergebnis.

Der gewichtete Mittelwert wird berechnet, indem für jeden Einzelverbrauchswert sein Anteil am Gesamtverbrauch berechnet wird. Dazu wird die zugehörige Strecke durch die Gesamtfahrstrecke geteilt und dann mit dem Kraftstoffverbrauchswert multipliziert. Der Mittelwert ist dann die Summe aller Produkte aus Einzelverbrauch und dem dazugehörigen Streckenfaktor.
Berechnung des gewichteten Mittelwertes
Zur Berechnung des gewichteten Durchschnitts in Microsoft Excel kannst du die Summenprodukt-Formel verwenden.
=SUMMENPRODUKT(A1:A10, B1:B10)
Spalte A der Excel-Tabelle enthält die einzelnen Verbrauchswerte. In Spalte B musst du das Gewicht für jeden einzelnen Wert berechnen. Dies ist die entsprechende Distanz, dividiert durch die Gesamtdistanz.
In meinem Beispiel sieht das dann so aus:
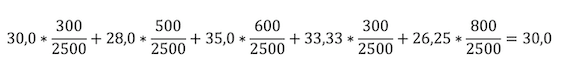
Du siehst, hier kommt das gleiche Ergebnis, wie bei der Berechnung des Gesamtverbrauches heraus. Also ist auch diese Methode genau.
Ich halte die Gesamtverbrauchsberechnung für praktikabler und würde sie deshalb dem gewichteten Mittelwert vorziehen.
Im Augenblick fällt mir keine Situation ein, wo ich diese Methode anwenden würde.
Eventuell, wenn nur die Verbrauchsangaben aus dem Fahrzeug und die Kilometerstände vorliegen und die getankten Dieselmenge nicht.
Mit der Standardabweichung eine Kennzahl für die Streuung ausrechnen.
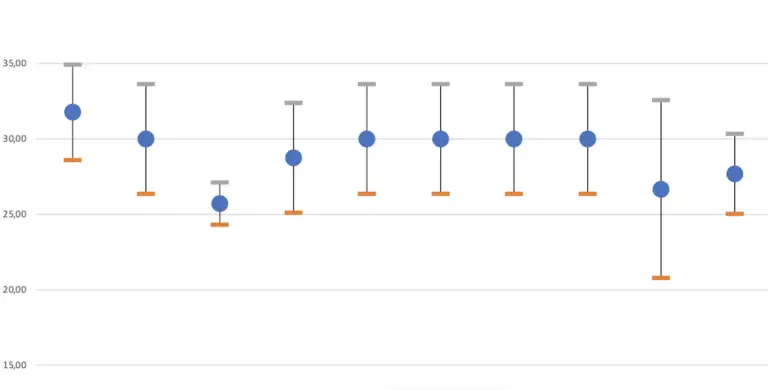
Zu guter Letzt solltest du überprüfen, wie stark die Einzelverbrauchswerte um den Durchschnittsverbrauch streuen.
Es ist logisch. Um so enger die Werte alle beieinander liegen, um so wahrscheinlicher ist der Durchschnittswert wirklich repräsentativ.
Sind die Einzelwerte weit auseinander, dann besteht die Gefahr, dass der Durchschnittsverbrauch einen größeren Fehler beinhaltet und deshalb nicht repräsentativ ist.
Im Artikel: Wie du die Streuung von Verbrauchswerten kontrollierst, beschreibe ich genau, wie du die Streuung der Verbrauchswerte berechnen kannst und wie du damit die Genauigkeit des Durchschnittsverbrauches überprüfen kannst.
Also schau die bitte unbedingt rein!
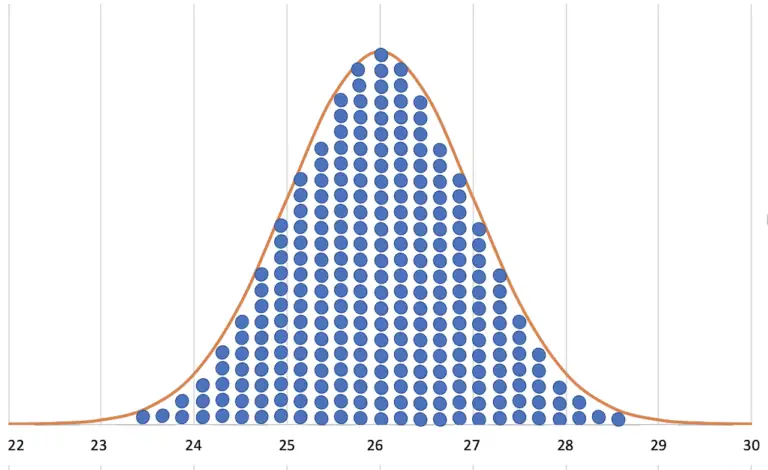
Im Artikel: Die Normalverteilung – so lässt sich der Zufall berechnen, erfährst du die theoretischen Grundlagen, warum das alles so funktioniert.
Auch der Artikel: Warum der Kraftstoffverbrauch streut. (einfach erklärt), ist in diesem Zusammenhang lesenswert.
Zusammenfassung
Hat dir der Artikel gefallen? Schreib mir doch bitte im Kommentar dein Feedback. Mich interessiert auch, worüber ich noch schreiben sollte.