Kräfte aufteilen und zusammenfassen | Schritt-für-Schritt-Anleitung

Kräfte werden mit diesen beiden Formeln in ihre rechtwinkligen Komponenten aufgeteilt:

Fx = cos(α) * F

Fy = sin(α) * F

Die Komponenten mit gleicher Kraftrichtung dürfen addiert und subtrahiert werden.

Bei der Kraftstoff- und Energieverbrauchsoptimierung ist es hilfreich, Kräfte in ihrer Größe und Wirkrichtung kennen.

Leider ist es nicht eine Kraft allein, sondern es wirken mehrere Kräfte gleichzeitig.

Um das Zusammenwirken aller dieser Kräfte zu erkennen, musst du sie zusammenführen.

Dem stehen aber oft unterschiedliche Kraftrichtungen entgegen, denn du darfst nur Kräfte mit gleicher Richtung zusammenfassen.

Diese Aufgabe kommt in der Praxis sehr häufig vor. Auch in meinem Blog werden wir in vielen Artikeln Kräfte in die richtige Richtung bringen müssen. Sei es, wenn wir über die Fahrwiderstände reden oder aber wenn wir uns mit Kräften im Triebstrang befassen.

Hier in diesem Artikel erkläre ich die Vorgehensweise und die Formeln, mit denen du Kräfte umformst und zusammenfasst.

Mit dem Onlinerechner kannst du die Kraftkomponenten schnell ausrechnen.

Wenn du den Artikel gelesen hast, dann bist du auf die Aufgaben gut vorbereitet, die dich in den anderen Artikeln erwarten.

Die Kräfte selbst habe ich im Artikel: Kraft – unsichtbar, aber allgegenwärtig beschrieben. Die Addition und Subtraktion von Kräften habe ich da ausgelassen, diesen Teil findest du nun hier.

Nur Kräfte mit gleicher Richtung dürfen addiert oder subtrahiert werden.

Kräfte sind Vektorgrößen. Das bedeutet, sie haben eine Richtung.

Die Wirkung von Kräften hat immer eine Richtung. Es sind Bewegungs- oder Verformungsrichtungen, die du beobachten kannst.

Wenn das so ist, dann ist es auch logisch, dass die Kräfte, welche die Ursache für die Wirkung sind, selber auch eine Richtung haben.

Es ist extrem hilfreich, die Richtung der Kräfte zu erkennen, obwohl die Kraft selber ja unsichtbar ist.

Also ist es richtig und gut, dass Kräfte eine Richtung haben, denn nur dadurch können wir Bewegungs- und Verformungsrichtungen beeinflussen.

Wenn du das im Kopf hast, dann ist es doch auch logisch, dass Kräfte zusammengezählt werden können, wenn sie in die gleiche Richtung zeigen, denn dann vergrößert sich dadurch die Wirkung in dieser Richtung.

Falls die Wirkrichtungen der Kräfte nicht übereinstimmen oder die Wirkrichtungen nicht zu der interessierenden Bewegungs- oder Verformungsrichtung passen, dann musst du die Kräfte in die relevanten Komponenten zerlegen.

Nur diese Komponenten sind dann für dein Ziel oder deine Frage relevant.

Also schauen wir uns nun an, wie Kräfte zerlegt werden, um die Anteile finden, die in die interessierende Richtung wirken und die addiert oder subtrahiert werden können.

Am Anfang steht das Koordinatensystem.

Am Anfang jeder Betrachtung steht immer die Überlegung, welche Wirkrichtungen untersucht werden sollen. Danach müssen die Kräfte entsprechend dieser Wirkrichtungen in ihre Komponenten zerlegt werden.

Bei einem Fahrzeug interessiert die Fahrtrichtung.

In Fahrtrichtung wirken Antriebskräfte und Fahrwiderstände.

Das sind dann auch die Kraftkomponenten, mit denen wir uns hier in diesem Blog immer wieder intensiv auseinandersetzen werden, weil sie für den Energieverbrauch ausschlaggebend sind.

Dann sind natürlich auch die Kräfte quer zur Fahrtrichtung interessant, weil diese die Fahrtrichtung verändern.

Bleibt dann noch die Hochrichtung übrig.

Damit haben wir ein rechtwinkliges Fahrzeug-Koordinatensystem gefunden, mit dem wir arbeiten können.

Im Triebstrang orientieren wir uns an Wellen und Reibflächen.

Wenn du dich innerhalb vom Triebstrang befindest, dann orientierst du dich an den Drehachsen von Wellen und der Orientierung von Reibflächen.

Bei drehenden Teilen ist ja in der Regel immer Rechtwinkligkeit gegeben, da sich die Bauteile um eine Mittellinie drehen.

So eine Drehachse ist zum Beispiel die Mitte der Kurbelwelle und eine Reibfläche ist die Zylinderlauffläche.

Es gibt aber natürlich noch unendlich viele weitere Möglichkeiten, um Koordinatensysteme zu definieren.

Währende der Entwicklungsphase legt der Konstrukteur für jedes einzelne Bauteil ein eigenes Koordinatensystem fest, welches für die Berechnung der auf das Teil wirkenden Kräfte benutzt wird.

Wo greifen die Kräfte an?

Hast du nun dein Koordinatenkreuz gefunden, dann musst du dir überlegen, wo der Nullpunkt des Koordinatensystems (auch Koordinatenursprung genannt) sinnvollerweise liegen soll.

Dafür gibt es unterschiedliche Möglichkeiten, die sich nach der Art der Kraft richten.

Kraftangriffspunkt

Findest du eine markante Stelle, an der eine Kraft von außen an deinem Körper angreift, dann legst du das Koordinatenkreuz genau an die Stelle.

Das kann zum Beispiel die Mitte des Radaufstandspunktes vom Reifen auf der Straße sein.

Ein anderes Beispiel ist die Mitte des Königszapfenlagers in der Sattelkupplung vom LKW. An dieser Stelle werden die Kräfte von der Zugmaschine auf den Auflieger übertragen.

An den Kraftangriffspunkten kannst du meistens auch den Winkel finden, unter dem die Kraft einwirkt. Es ist wichtig, diesen Winkel zu kennen. Das werden wir gleich noch sehen.

Massenschwerpunkt

Bei Kräften, die von der Masse des Körpers abhängig sind, bietet es sich an, den Koordinatenursprung in den Massenschwerpunkt zu legen.

Was ist ein Massenschwerpunkt?

Stell dir den Körper als eine Ansammlung von vielen, vielen kleinen Würfeln vor und an jedem Würfel wirkt genau die Kraft, die seiner Masse entspricht.

Nun drückst du deinen Körper gedanklich so stark zusammen, dass sich alle Würfel mit ihrer kompletten Masse in einem einzigen, winzig kleinen Würfel vereinigen.

Dann sind auch alle einzelnen Kräfte zu einer einzigen Summenkraft zusammengeführt.

Mit dieser einen, konkreten Kraft kannst du viel einfacher arbeiten, als mit den vielen über den ganzen Körper verteilten Minikräften.

Kräfte, für die diese Vorgehensweise sinnvoll ist, sind zum Beispiel die Gewichtskraft, die Trägheitskraft und die Fliehkraft.

Die Lage des Schwerpunktes kann experimentell oder rechnerisch ermittelt werden. Das ist für viele Anwendungsfälle auch notwendig.

Auf vielen Ladungsstücken ist der Massenschwerpunkt auf der Kiste gekennzeichnet.

Hier schauen wir uns nur geradlinigen Bewegungen an. Da ist es vertretbar, wenn du die Lage des Schwerpunktes nur ungefähr abschätzt. Bei geradlinigen Bewegungen (Translation) und Verformungen ist nur die Richtung der Kräfte ausschlaggebend, nicht die exakte Position.

Das ändert sich in dem Moment, in dem es um Drehbewegungen und Biegung eingeht. Darüber schreibe ich in einem eigenen Artikel.

Flächenschwerpunkt

Kräfte, die durch Druck auf eine Fläche entstehen, stellen einen ähnlichen Sachverhalt dar.

Auch hier kannst du dir viele, viele kleine Quadrate vorstellen, von denen jedes eine Kraft trägt, die seiner Fläche entspricht.

Wenn du nun alles auf ein kleines Quadrat in der geometrischen Mitte der Körperoberfläche zusammenfasst, dann hast du den Flächenschwerpunkt, der als Angriffspunkt der Summenkraft verwendet werden kann.

Beispiel für solche Kräfte sind die Kolbenkraft und der Luftwiderstand.

Schnittpunkt von Kräften

Hast du es mit mehreren Kräften zu tun, dann ist es hilfreich, wenn alle Kräfte in ein gemeinsames Koordinatenkreuz verschoben werden können.

Kräfte können entlang ihrer Wirkungslinie verschoben werden.

Das machst du dir zunutze und legst den Nullpunkt des Koordinatenkreuzes in den Schnittpunkt der Wirklinien deiner Kräfte.

Wenn du mehrere Kräfte hast, die keinen gemeinsamen Schnittpunkt ihrer Wirklinien haben oder wo der Schnittpunkt weit außerhalb deines Körpers liegt, dann darfst du Kräfte, unter bestimmten Voraussetzungen, auch parallel in einen Punkt verschieben.

Achtung:

• Das geht nur hier bei geradliniger Bewegung. Bei Drehbewegung oder Biegung geht das nicht so einfach.
• Parallelverschiebung bedeutet, dass der Winkel der Wirklinie der Kraft nicht verändert werden darf!

Kräfte aufteilen

Jetzt haben wir also ein Koordinatensystem mit den interessanten Richtungen, den Koordinatenursprung und die Kraft im Koordinatenursprung.

Nun wollen wir die Kraft in die Kraftkomponenten aufteilen, die entlang unserer Koordinatenachsen wirken.

Dafür suchen wir uns jeweils die Fläche, in der die interessierende Kraftrichtung und die Kraft selber liegen.

Da wir uns ein rechtwinkliges Koordinatensystem gegeben haben, finden wir zwischen Kraft und Koordinatenachse immer ein rechtwinkliges Dreieck, in dem wir die Winkelfunktionen anwenden können.

Nachdem du die Komponenten aller Kräfte berechnet hast, kannst du jeweils alle Kräfte einer Richtung zusammenzählen. Aber Achtung, bitte das Vorzeichen beachten!

Als Resultat hast du nun 3 Kräfte, für jede Richtung des Koordinatenkreuzes eine.

Diese Kräfte sind rechtwinklig zueinander und beeinflussen sich somit nicht.

Der richtige Winkel ist wichtig.

In den allermeisten Fällen wird sich die Kraft in einer Fläche des Koordinatensystems befinden.

Meistens sind Teilkomponenten der Kräfte einfacher zu finden, als die eigentliche Gesamtkraft. Das hilft ungemein, weil dann diese Teilkomponenten nur im Zweidimensionalen in eine Richtung gebracht werden müssen.

Denke zum Beispiel an den Luftwiderstand.

• Weht der Wind schräg von der Seite, dann liegt die entsprechende Kraft in der xy – Ebene und die Windrichtung gibt dir den Winkel.
• Zusätzlich gibt es dann aber noch den Fahrtwind, der gerade von vorn kommt und sich auch in der xy – Ebene befindet, allerdings aus einer anderen Richtung kommt.

Wir werden sehr häufig das Glück haben, dass so eine Situation zu Hilfe kommt.

Du musst in diesen Fällen den Winkel herausfinden, der zwischen der Kraft und einer der Koordinatenachsen besteht. Dann kannst du beide Kraftkomponenten ausrechnen.

Es gibt aber natürlich trotzdem den Fall, dass die Kraft irgendwo hinzeigt, nur leider nicht entlang der Ebenen unseres Koordinatensystems.

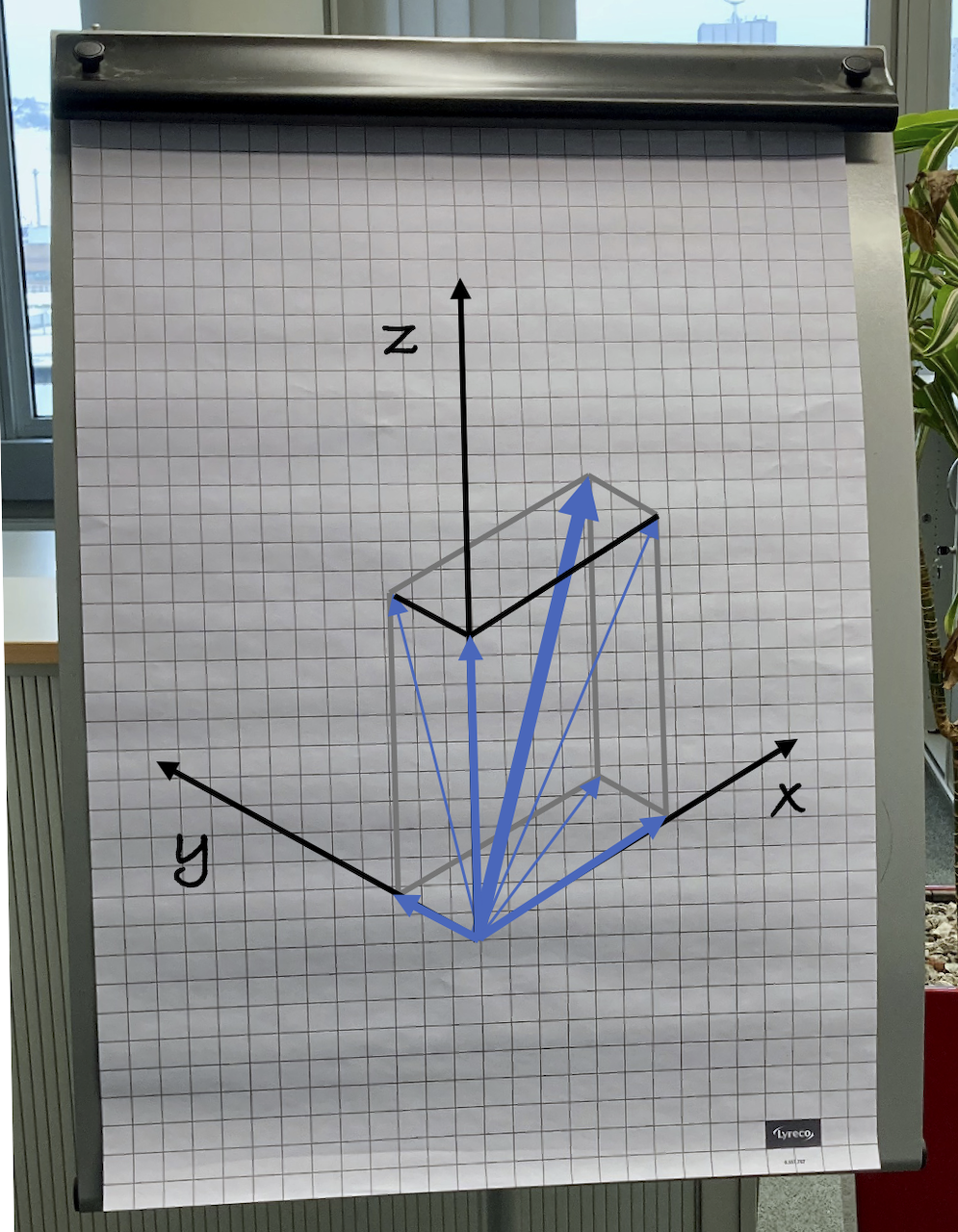
Ich habe dir hier in diesem Bild so einen Fall aufgezeichnet.

Die drei schwarzen Pfeilen sind die Kraftkomponenten entlang der Achsen des Koordinatensystems, die wir suchen. Sie sind genau rechtwinklig zueinander.

Die dunkelblaue Kraft ist unsere Ausgangskraft, sie zeigt in den Raum.

1. Variante

Um von der blauen auf die schwarzen Kräfte zu kommen, musst du die Ebenen suchen, auf der jeweils eine Achse des Koordinatensystems und die Kraft selber liegt. Im Bild ist das die blaue Ebene.

(Ich habe jeweils nur immer ein Ebene gezeichnet, damit das Bild nicht unübersichtlich wird.)

Da sich die Kraft und die Achse im Koordinatenursprung treffen, gibt es immer so eine Ebene.

In dieser Ebene misst du den Winkel zwischen Kraft und Achse.

Das machst du dreimal, jeweils für die entsprechende Achse, deren Kraftkomponenten gesucht ist.

Mit den drei Winkeln und der obenstehenden Formel kannst du nun die 3 Kraftkomponenten berechnen.

2. Variante

Kannst du diese Winkel nicht direkt herausfinden, dann versuche einen anderen Weg.

Wenn du den Winkel herausfindest, unter dem die Kraft und eine Ebene des Koordinatensystems zueinander stehen, dann kannst du die Kraft rechnerisch in diese Ebene projizieren.

In dem Beispielbild ist es die gelbe Fläche, die senkrecht auf einer der Koordinatenebenen steht.

Mit diesem Winkel kannst du nun die gelben Teilkräfte ausrechnen, die in den Koordinatenebenen liegen. Das musst du für zwei Koordinatenebenen machen.

Nun brauchst du noch den Winkel dieser Teilkräfte zu jeweils einer der Achsen (in der grauen Ebene) und du kannst im zweiten Schritt diese Kraftkomponenten auf die Achsen aufteilen.

3. Variante

Eine dritte Alternative ist die Vektorrechnung, für die du den Einheitsvektor der Kraft brauchst. Also auch nicht wirklich einfach.

Das ist schon ziemlich umständlich, denn unglücklicherweise sind die Winkel alle unterschiedlich.

Dieser Fall kommt glücklicherweise eher selten vor. In unseren Anwendungsfällen hier in diesem Blog werden wir das nicht brauchen.

Zusammenfassung

Schreibe mir doch bitte im Kommentar, wie dir die Erklärung gefallen hat!

Alle Berechnungen sind ohne juristische Gewähr auf Richtigkeit.